Mudanças entre as edições de "Map2321"

Edição das 21h35min de 15 de janeiro de 2013

Aspectos históricos da teoria de Controle

Em praticamente todos os sistemas da natureza há a possibilidade de intervenção que permite exercer algum controle sobre o sistema. Aspectos tecnológicos nos fazem procurar uma forma de exercer este controle automaticamente. É o que chamaremos de retroalimentação do sistema.

Basicamente a origem da teoria de controle são os sistemas de regulagem, isto é, procura-se desenvolver um processo automático para que um sistema fique numa situação de equilíbrio. Assim um sensor detecta se o sistema está se desregulando e um controlador atuaria automaticamente para restabelecer o equilibrio. Claro que muitos mecanismos engenhosos foram desenvolvidos durante milênios para resolver este problema, porém um caso interessante era o de controle de velocidade de moinhos de vento. Huygens inventou um instrumento conhecido como flyball que na pratica resolvia o problema. Esta mesma idéia do flyball foi usada depois por Watt em máquinas para o controle de fluxo de vapor. Este modelo que funcionava na prática tinha um problema de excesso de vibração para velocidades muito altas. Foi Maxwell quem elaborou um modelo matemático para o flyball e colocou o problema de eliminação das vibrações como um problema de estabilização. Este foi, pode-se dizer, o primeiro problema matemático da teoria de controle.

No começo do século XX, o desenvolvimento das redes de comunicações telefônicas, propiciou o aparecimento de novos modelos e a utilização de métodos da teoria de funções a variáveis complexas para eliminação de ruídos e filtragens de sinais. Os trabalhos pioneiros nesta linha deveu-se a Black, Bode e Nyquist do grupo do laboratório Bell. O conjunto de métodos desenvolvidos por eles influenciou bastante a engenharia e é chamado de teoria de controle clássica. Isso foi mais ou menos em 1930. Depois da segunda guerra mundial os métodos de otimização ganharam importância e é um mérito da teoria de Pontriaguin o estudo da teoria de controle ótimo. O desenvolvimento da teoria de sistemas dinâmicos propiciou uma nova abordagem para os sistemas de controles lineares. Assim nas décadas de 1960 e 1970 desenvolveu-se bastante uma teoria estrutural dos sistemas de controle. E nesta abordagem "moderna" baseada no espaço de estados dos sistemas são importantes os conceitos de controlabilidade e observabilidade introduzidos por Kalman. No final do século passado desenvolveram-se os métodos geometricos para o estudo de sistema de controle não linear. Em todos estes tópicos há ainda pesquisa bastante ativa. --Patonelli 15h27min de 24 de agosto de 2009 (UTC)patonelli

Exemplos de sistemas de controle

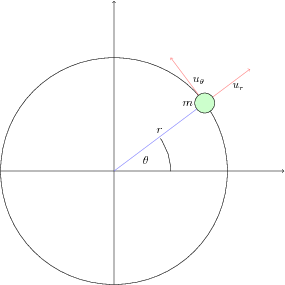
Um satélite simples num campo newtoniano

satélite num campo newtoniano

Uma partícula de massa $m$ está sob ação de um campo de acelerações central newtoniano. Além disso podemos colocar dois controles independentes, um na direção radial e outro na direção tangencial $u_{r}$ e $u_{\theta}$ respectivamente. A equação dinâmica deste sistema é dada pela segunda lei de Newton:

fazendo a massa $m=1$ para que eu não tenha que ficar digitando coisas a mais. Podemos reecrever as equações em coordenadas polares como:

Estas duas equações nos dão um sistema de controle não linear com duas entradas de controle. Voltaremos a este exemplo quando falarmos de linearização.

--Patonelli 21h10min de 22 de agosto de 2009 (UTC)patonelli

O pêndulo invertido

Esquema de um pêndulo invertido num carrinho

O pêndulo invertido é um problema clássico em teoria de controle, as equações do movimento são:

A variável de controle aqui é a força $F$

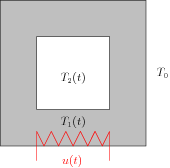
Um forno simplificado

forno simplificado

A figura mostra o esquema de um forno constituído de uma jaqueta de um material (a parte cinza) que é aquecido por uma resistência, e o calor é transmitido para o interior do forno. A taxa de calor $u(t)$ é o controle do sistema. As temperaturas (que estamos supondo ser uniformemente distribuídas no espaçao!) $T_1(t)$ e $T_2(t)$ são as variáveis de estados. Sendo $c_1$ e $c_2$ as capacidades térmicas da jaqueta e do interior do forno respectivamente; $a_1$ e $a_2$ área exterior e interior da jaqueta; $r_1$ e $r_2$ os coeficientes de transmissão de calor da parte externa e interna da jaqueta e $T_0$ a temperatura exterior. A equação de balanço térmico nos dá:

Onde $x_1=T_1-T_0$ e $x_2=T_2-T_0$

Um circuito elétrico

equações dos componentes elétricos

Na figura ao lado vemos as equações dinâmicas de alguns componentes elétricos: resistores, condensadores e indutores. Usaremos estas equações e as leis de Kirchoff dos nós e das malhas para escrever a relação dinâmica entre voltagem e corrente do circuito abaixo.

Circuito do exemplo

Chamaremos de $x_1$ a voltagem pelo capacitor $C$ do circuito, e de $x_2$ a corrente através do indutor $L$ Aplicando as leis constitutivas dos elementos e as leis de Kirchoff temos as relações dinâmicas

Neste caso $v(t)$ é a única entrada do sistema (e portanto o controle) e a corrente é a saída do sistema. Para encontrar a relação entre entrada e saída temos resolver uma equação diferencial nas variáveis $x_1$ e $x_2$, que podem ser interpretadas como variáveis auxiliares neste caso. --Patonelli 21h32min de 22 de agosto de 2009 (UTC)patonelli

Um modelo de economia

Num modelo simples podemos definir as seguintes variáveis $$Y_n$$ é a receita anual no ano $n$

$C_n$ total do consumo no ano $n$
$I_n$ investimento no ano
$G_n$ gastos do governo

A equação dinâmica é determinada pelas seguintes relações entre as variáveis

O controle do sistema é $G_n$. A equação a diferenças finitas fica

--Patonelli 23h04min de 22 de agosto de 2009 (UTC)patonelli

Caracterização dos sistemas lineares

Os exemplos acima nos dão as principais carecterísticas dos sistemas de controle. Dependendo do sistema ser contínuo ou discreto temos as equações

e no caso discreto

onde $x\in \mathbb{R}^n$ é a variável de estado, $y\in \mathbb{R}^p$ é a variável de saída e $u\in \mathbb{R}^m$ são os parâmetros de entrada.

As funções estruturais do sistema $f:\mathbb{R}^n\times \mathbb{R}^m \to \mathbb{R}^n$ e $g:\mathbb{R}^n\times \mathbb{R}^m \to \mathbb{R}^p$ são usadas para classificar os sistemas. No nosso caso estaremos interessado somente nos casos de sistemas lineares invariantes no tempo, ou seja quando

Com $A$ matriz $n\times n$, $B$ matriz $n\times m$ e $C$ matriz $p\times n$. Nas próximas sessões vamos analisar mais detalhadamente estes exemplos.

Uma técnica de linearização

Se $(x_0,u_0)$ for um ponto de equilíbrio do campo $f(x,u)$ então o sistema

é o sistema linearizado em torno do ponto de equilíbrio. A mesma técnica é utilizada para o ponto de equilíbrio de um sistema discreto. Lembro que o ponto de equilíbrio de um sistema discreto satisfaz $f(x_0,u_0)= x_0$ e do sistema contínuo $f(x_0,u_0)= 0$

Como exemplo retomamos a equação do satélite. fazendo $u_{\theta}=u_r=0$, encontramos um movimento circular uniforme que é uma trajetória de equilíbrio para um determinado momento angular $$r(t)=r_0, \theta(t)=\omega t$$ Agora fazemos as mudanças de variáveis:

e usando a técnica de linearização ensinada obtemos os sistema linear:

Exponencial de matrizes

Defineremos a exponencial de uma matriz $A=(a_{ij})\in \mathbb{R}^{n\times n}$ como a soma da série:

Esta soma converge absolutamente uma vez que introduzimos no espaço das matrizes a norma induzida da norma euclidiana em $\mathbb{R}^n$ isto é

As principais propriedades da exponencial de matrizes:

Solução das equações lineares não homegêneas

Em primeiro lugar note que pela propriedade 6 acima a curva $$x(t)=\exp(tA)v$$ é solução da equação diferencial

para que satisfaça também a condição inicial $x(t_0)=x_0$ basta escolher $v=\exp(-t_0A)x_0$ desta forma

Da mesma forma para resolvermos o problema não homogêneo:

Notemos que a curva $$x(t)=\exp(tA)v(t)$$ satisfaz a equação: $$\dot{x}=Ax + \exp(tA)\dot{v}(t)$$ Resolvendo a equação em $v(t)$ $$\exp(tA)\dot{v}(t)=Bu(t)$$ $$\exp(t_0A)v(t_0)=x_0$$ obtemos $$v(t)=x_0+\int_{t_0}^t\exp(-sA)Bu(s)ds$$ e finalmente obtemos a nossa aplicação de transição de estados

Exemplo simples

Esboço das trajetórias usando controles constantes u=1 e u=-1

O sistema $\ddot{\mathbf{x}}=u(t)$ pode ser escrito como:

A aplicação da fórmula para a condição inicial no instante $t=0$, lembrando que $\exp(tA)=\begin{pmatrix} 1 & t \\ 0 & 1 \end{pmatrix}$, nos dá

Controlabilidade

Antes de abordar controlabilidade convém falar de dois tópicos:

Controles admissíveis

Translação nos controles

Concatenação de controles

A controlabilidade estuda a relação entre os controles e os pontos atingíveis no espaço de estados. Por isso é importante dar algumas propriedades estruturais do conjunto dos controles. Nesta disciplina chamaremos de Conjunto dos controles admissíveis o seguinte:

Este conjunto tem as seguintes propriedades:

1. É um espaço vetorial,
2. É invariante pelo sistema dinâmico de translação $\theta_t$
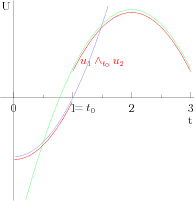
3. É fechado pela concatenação $\wedge_{t_0}$ para todo $t_0\in \mathbb{R}$
4. Contém a família das funções constantes por partes

Um subconjunto de $\mathcal{U}$ com estas quatro propriedades também pode ser chamado de um conjunto de controles admissíveis e alteraria um pouco o estudo da controlabilidade. Este conjunto que vamos usar pode ser pensado como o maior conjunto de controles admissíveis.

A translação é definida como:

e a concatenação no tempo $t_0$ é definida assim

Propriedades da aplicação de transição de estados

Para os sistemas de controle contínuos de forma geral, aplicação de transição de estados é uma aplicação:

Satisfazendo as propriedades:

• $\phi(t,t,x_0,u(\cdot))=x_0$, chamada de compatibilidade.
• $\phi(t_2, t_1, \phi(t_1,t_0,x_0,u(\cdot)),v(\cdot))=\phi(t_2,t_0,x_0,u\wedge_{t_1}v(\cdot))$, sistema dinâmico.
• $\phi(t_1,t_0,x_0,u(\cdot))$ só depende do valor de $u(t)$ no intervalo $[t_0,t_1]$

No caso dos sistemas lineares independentes do tempo temos

e neste caso temos ainda as seguintes propriedades:

• $\phi(t,t_0,x_0,u(\cdot)) =\phi(t,t_0,x_0, 0) + \phi(t_1,t_0,0,u(\cdot))$: decomposição entre dinâmica livre e controlada
• $\phi(t,t_0,x_0 + x_1,u(\cdot)+ v(\cdot)) = \phi(t,t_0,x_0,u(\cdot))+ \phi(t,t_0,x_1,v(\cdot))$: princípio da superposição
• $\phi(t,t_0,x_0,\theta_{t_0}u(\cdot))= \phi(t-t_0,0,x_0,u(\cdot))$: invariante no tempo.

Esta última propriedade é que nos justifica o estudo da controlabilidade só quando o tempo inicial é $0$

Se $a$ e $b$ são dois pontos do espaço de estados $\mathbb{R}^n$, dizemos que $b$ é atingível em tempo $T$ a partir de $a$ se existir um controle admissível $u(t)\in \mathcal{U}$ tal que

Nesta caso dizemos também que o controle $u$ transfere $a$ para $b$ em tempo $T$. O conjunto de todos os pontos atingíveis a partir de $a$ em tempo $T>0$ será denotado por $\mathcal{A}(a,T)$.

No caso do sistema linear é fácil verificar que

Diremos que o sistema é controlável quando $\mathcal{A}(0,T) = \mathbb{R}^n$.

Matriz de controlabilidade

Note que o conjunto $\mathcal{A}(0,T)$ depende apenas das matrizes $A$, $B$ do tempo $T>0$ e da família de controles admissíveis. Quando o sistema for controlável diremos que o par $(A,B)$ é controlável.

Definiremos a matriz de controlabilidade de $(A,B)$ (ou do sistema ) como

esta matriz é simétrica, semidefinida positiva. Se for definida positiva então é invertível e neste caso o par $(A,B)$ é controlável.

Basta verificar que para qualquer vetor do espaço de estados $\mathbf{b} \in \mathbb{R}^n$ temos que o controle

transfere a origem para $\mathbf{b}$ em tempo $T$

Assim $Q_T$ ser invertível é uma condição suficiente para a controlabilidade. veremos que é também necessária.

Se o núcleo $Q_T$ tem um elemento $\mathbf{v} \neq 0$ então $<Q_T\mathbf{v},\mathbf{v}> = \int_0^T ||B^\prime \exp(sA^\prime)\mathbf{v}||^2ds=0$. Pela analiticidade do integrando temos $B^\prime \exp(sA^\prime)\mathbf{v} = 0 \forall s$.

Neste caso temos que para todo controle admissível $u(\cdot)\in \mathcal{U}$

e isto significa que o vetor $\mathbf{v}$ não é acessível pois é ortogonal ao conjunto de atingibilidade de $0$. Portanto para o sistema ser controlável é necessário que a matriz $Q_T$ seja invertível.

Exercício resolvido

Verificar se é controlável o seguinte sistema:

O polinômio $p(z)$ com todos os coeficientes positivos é estável se e somente se a matriz de Routh tem exatamente $n+1$ linhas 
com o primeiro termo não nulo e todos os termos da primeira coluna são positivos.