Mudanças entre as edições de "Map2321"

Edição atual tal como às 18h10min de 14 de agosto de 2013

[editar] Aspectos históricos da teoria de Controle

Em praticamente todos os sistemas da natureza há a possibilidade de intervenção que permite exercer algum controle sobre o sistema. Aspectos tecnológicos nos fazem procurar uma forma de exercer este controle automaticamente. É o que chamaremos de retroalimentação do sistema.

Basicamente a origem da teoria de controle são os sistemas de regulagem, isto é, procura-se desenvolver um processo automático para que um sistema fique numa situação de equilíbrio. Assim um sensor detecta se o sistema está se desregulando e um controlador atuaria automaticamente para restabelecer o equilibrio. Claro que muitos mecanismos engenhosos foram desenvolvidos durante milênios para resolver este problema, porém um caso interessante era o de controle de velocidade de moinhos de vento. Huygens inventou um instrumento conhecido como flyball que na pratica resolvia o problema. Esta mesma idéia do flyball foi usada depois por Watt em máquinas para o controle de fluxo de vapor. Este modelo que funcionava na prática tinha um problema de excesso de vibração para velocidades muito altas. Foi Maxwell quem elaborou um modelo matemático para o flyball e colocou o problema de eliminação das vibrações como um problema de estabilização. Este foi, pode-se dizer, o primeiro problema matemático da teoria de controle.

No começo do século XX, o desenvolvimento das redes de comunicações telefônicas, propiciou o aparecimento de novos modelos e a utilização de métodos da teoria de funções a variáveis complexas para eliminação de ruídos e filtragens de sinais. Os trabalhos pioneiros nesta linha deveu-se a Black, Bode e Nyquist do grupo do laboratório Bell. O conjunto de métodos desenvolvidos por eles influenciou bastante a engenharia e é chamado de teoria de controle clássica. Isso foi mais ou menos em 1930. Depois da segunda guerra mundial os métodos de otimização ganharam importância e é um mérito da teoria de Pontriaguin o estudo da teoria de controle ótimo. O desenvolvimento da teoria de sistemas dinâmicos propiciou uma nova abordagem para os sistemas de controles lineares. Assim nas décadas de 1960 e 1970 desenvolveu-se bastante uma teoria estrutural dos sistemas de controle. E nesta abordagem "moderna" baseada no espaço de estados dos sistemas são importantes os conceitos de controlabilidade e observabilidade introduzidos por Kalman. No final do século passado desenvolveram-se os métodos geometricos para o estudo de sistema de controle não linear. Em todos estes tópicos há ainda pesquisa bastante ativa. --Patonelli 15h27min de 24 de agosto de 2009 (UTC)patonelli

[editar] Exemplos de sistemas de controle

[editar] Um satélite simples num campo newtoniano

satélite num campo newtoniano

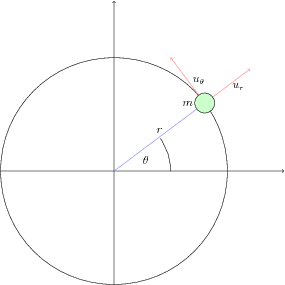
Uma partícula de massa $m$ está sob ação de um campo de acelerações central newtoniano. Além disso podemos colocar dois controles independentes, um na direção radial e outro na direção tangencial $u_{r}$ e $u_{\theta}$ respectivamente. A equação dinâmica deste sistema é dada pela segunda lei de Newton:

fazendo a massa $m=1$ para que eu não tenha que ficar digitando coisas a mais. Podemos reecrever as equações em coordenadas polares como:

Estas duas equações nos dão um sistema de controle não linear com duas entradas de controle. Voltaremos a este exemplo quando falarmos de linearização.

--Patonelli 21h10min de 22 de agosto de 2009 (UTC)patonelli

[editar] O pêndulo invertido

Esquema de um pêndulo invertido num carrinho

O pêndulo invertido é um problema clássico em teoria de controle, as equações do movimento são:

A variável de controle aqui é a força $F$

[editar] Um forno simplificado

forno simplificado

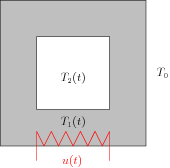
A figura mostra o esquema de um forno constituído de uma jaqueta de um material (a parte cinza) que é aquecido por uma resistência, e o calor é transmitido para o interior do forno. A taxa de calor $u(t)$ é o controle do sistema. As temperaturas (que estamos supondo ser uniformemente distribuídas no espaçao!) $T_1(t)$ e $T_2(t)$ são as variáveis de estados. Sendo $c_1$ e $c_2$ as capacidades térmicas da jaqueta e do interior do forno respectivamente; $a_1$ e $a_2$ área exterior e interior da jaqueta; $r_1$ e $r_2$ os coeficientes de transmissão de calor da parte externa e interna da jaqueta e $T_0$ a temperatura exterior. A equação de balanço térmico nos dá:

Onde $x_1=T_1-T_0$ e $x_2=T_2-T_0$

[editar] Um circuito elétrico

equações dos componentes elétricos

Na figura ao lado vemos as equações dinâmicas de alguns componentes elétricos: resistores, condensadores e indutores. Usaremos estas equações e as leis de Kirchoff dos nós e das malhas para escrever a relação dinâmica entre voltagem e corrente do circuito abaixo.

Circuito do exemplo

Chamaremos de $x_1$ a voltagem pelo capacitor $C$ do circuito, e de $x_2$ a corrente através do indutor $L$ Aplicando as leis constitutivas dos elementos e as leis de Kirchoff temos as relações dinâmicas

Neste caso $v(t)$ é a única entrada do sistema (e portanto o controle) e a corrente é a saída do sistema. Para encontrar a relação entre entrada e saída temos resolver uma equação diferencial nas variáveis $x_1$ e $x_2$, que podem ser interpretadas como variáveis auxiliares neste caso. --Patonelli 21h32min de 22 de agosto de 2009 (UTC)patonelli

[editar] Um modelo de economia

Num modelo simples podemos definir as seguintes variáveis,

$Y_n$ é a receita anual  no ano $n$
$C_n$ total do consumo no ano $n$
$I_n$ investimento no ano
$G_n$ gastos do governo

A equação dinâmica é determinada pelas seguintes relações entre as variáveis

O controle do sistema é $G_n$. A equação a diferenças finitas fica

--Patonelli 23h04min de 22 de agosto de 2009 (UTC)patonelli

[editar] Caracterização dos sistemas lineares

Os exemplos acima nos dão as principais carecterísticas dos sistemas de controle. Dependendo do sistema ser contínuo ou discreto temos as equações

e no caso discreto

onde $x\in \mathbb{R}^n$ é a variável de estado, $y\in \mathbb{R}^p$ é a variável de saída e $u\in \mathbb{R}^m$ são os parâmetros de entrada.

As funções estruturais do sistema $f:\mathbb{R}^n\times \mathbb{R}^m \to \mathbb{R}^n$ e $g:\mathbb{R}^n\times \mathbb{R}^m \to \mathbb{R}^p$ são usadas para classificar os sistemas. No nosso caso estaremos interessado somente nos casos de sistemas lineares invariantes no tempo, ou seja quando

Com $A$ matriz $n\times n$, $B$ matriz $n\times m$ e $C$ matriz $p\times n$. Nas próximas sessões vamos analisar mais detalhadamente estes exemplos.

[editar] Uma técnica de linearização

Se $(x_0,u_0)$ for um ponto de equilíbrio do campo $f(x,u)$ então o sistema

é o sistema linearizado em torno do ponto de equilíbrio. A mesma técnica é utilizada para o ponto de equilíbrio de um sistema discreto. Lembro que o ponto de equilíbrio de um sistema discreto satisfaz $f(x_0,u_0)= x_0$ e do sistema contínuo $f(x_0,u_0)= 0$

Como exemplo retomamos a equação do satélite. fazendo $u_{\theta}=u_r=0$, encontramos um movimento circular uniforme que é uma trajetória de equilíbrio para um determinado momento angular $$r(t)=r_0, \theta(t)=\omega t$$ Agora fazemos as mudanças de variáveis:

e usando a técnica de linearização ensinada obtemos os sistema linear:

Vamos considerar um segundo exemplo, das equações de Euler de um corpo rígido. As equações são as seguintes:

Vamos considerar $I_1=I_2$ e linearizar o sistema resultante em torno de $u_i=0$ e da trajetória particular $$\begin{gather} \omega_1(t) = \cos(K\omega_0 t) \\ \omega_2(t) = \sin(K\omega_0 t) \\ \omega_3(t) = \omega_0 \end{gather}$$

O sistema linearizado, ao longo desta trajetória fica:

Neste caso o sistema linear não é invariante no tempo!

[editar] Exponencial de matrizes

Defineremos a exponencial de uma matriz $A=(a_{ij})\in \mathbb{R}^{n\times n}$ como a soma da série:

Esta soma converge absolutamente uma vez que introduzimos no espaço das matrizes a norma induzida da norma euclidiana em $\mathbb{R}^n$ isto é $\newcommand{\norm}[1]{\| #1 \|}$

As principais propriedades da exponencial de matrizes:

[editar] Solução das equações lineares não homegêneas

Em primeiro lugar note que pela propriedade 6 acima a curva $$x(t)=\exp(tA)v$$ é solução da equação diferencial

para que satisfaça também a condição inicial $x(t_0)=x_0$ basta escolher $v=\exp(-t_0A)x_0$ desta forma

Da mesma forma para resolvermos o problema não homogêneo:

Notemos que a curva $$x(t)=\exp(tA)v(t)$$ satisfaz a equação: $$\dot{x}=Ax + \exp(tA)\dot{v}(t)$$ Resolvendo a equação em $v(t)$ $$\exp(tA)\dot{v}(t)=Bu(t)$$ $$\exp(t_0A)v(t_0)=x_0$$ obtemos $$v(t)=x_0+\int_{t_0}^t\exp(-sA)Bu(s)ds$$ e finalmente obtemos a nossa aplicação de transição de estados

[editar] Exemplo simples

Esboço das trajetórias usando controles constantes u=1 e u=-1

O sistema $\ddot{\mathbf{x}}=u(t)$ pode ser escrito como:

A aplicação da fórmula para a condição inicial no instante $t=0$, lembrando que $\exp(tA)=\begin{pmatrix} 1 & t \\ 0 & 1 \end{pmatrix}$, nos dá

[editar] Controlabilidade

Antes de abordar controlabilidade convém falar de dois tópicos:

[editar] Controles admissíveis

Translação nos controles

Concatenação de controles

A controlabilidade estuda a relação entre os controles e os pontos atingíveis no espaço de estados. Por isso é importante dar algumas propriedades estruturais do conjunto dos controles. Nesta disciplina chamaremos de Conjunto dos controles admissíveis o seguinte:

Este conjunto tem as seguintes propriedades:

1. É um espaço vetorial,
2. É invariante pelo sistema dinâmico de translação $\theta_t$
3. É fechado pela concatenação $\wedge_{t_0}$ para todo $t_0\in \mathbb{R}$
4. Contém a família das funções constantes por partes

Um subconjunto de $\mathcal{U}$ com estas quatro propriedades também pode ser chamado de um conjunto de controles admissíveis e alteraria um pouco o estudo da controlabilidade. Este conjunto que vamos usar pode ser pensado como o maior conjunto de controles admissíveis.

A translação é definida como:

e a concatenação no tempo $t_0$ é definida assim

[editar] Propriedades da aplicação de transição de estados

Para os sistemas de controle contínuos de forma geral, aplicação de transição de estados é uma aplicação:

Satisfazendo as propriedades:

• $\phi(t,t,x_0,u(\cdot))=x_0$, chamada de compatibilidade.
• $\phi(t_2, t_1, \phi(t_1,t_0,x_0,u(\cdot)),v(\cdot))=\phi(t_2,t_0,x_0,u\wedge_{t_1}v(\cdot))$, sistema dinâmico.
• $\phi(t_1,t_0,x_0,u(\cdot))$ só depende do valor de $u(t)$ no intervalo $[t_0,t_1]$

No caso dos sistemas lineares independentes do tempo temos

e neste caso temos ainda as seguintes propriedades:

• $\phi(t,t_0,x_0,u(\cdot)) =\phi(t,t_0,x_0, 0) + \phi(t_1,t_0,0,u(\cdot))$: decomposição entre dinâmica livre e controlada
• $\phi(t,t_0,x_0 + x_1,u(\cdot)+ v(\cdot)) = \phi(t,t_0,x_0,u(\cdot))+ \phi(t,t_0,x_1,v(\cdot))$: princípio da superposição
• $\phi(t,t_0,x_0,\theta_{t_0}u(\cdot))= \phi(t-t_0,0,x_0,u(\cdot))$: invariante no tempo.

Esta última propriedade é que nos justifica o estudo da controlabilidade só quando o tempo inicial é $0$

Se $a$ e $b$ são dois pontos do espaço de estados $\mathbb{R}^n$, dizemos que $b$ é atingível em tempo $T$ a partir de $a$ se existir um controle admissível $u(t)\in \mathcal{U}$ tal que

Nesta caso dizemos também que o controle $u$ transfere $a$ para $b$ em tempo $T$. O conjunto de todos os pontos atingíveis a partir de $a$ em tempo $T>0$ será denotado por $\mathcal{A}(a,T)$.

No caso do sistema linear é fácil verificar que

Diremos que o sistema é controlável quando $\mathcal{A}(0,T) = \mathbb{R}^n$.

[editar] Matriz de controlabilidade

Note que o conjunto $\mathcal{A}(0,T)$ depende apenas das matrizes $A$, $B$ do tempo $T>0$ e da família de controles admissíveis. Quando o sistema for controlável diremos que o par $(A,B)$ é controlável.

Definiremos a matriz de controlabilidade de $(A,B)$ (ou do sistema ) como

esta matriz é simétrica, semidefinida positiva. Se for definida positiva então é invertível e neste caso o par $(A,B)$ é controlável.

Basta verificar que para qualquer vetor do espaço de estados $\mathbf{b} \in \mathbb{R}^n$ temos que o controle

transfere a origem para $\mathbf{b}$ em tempo $T$

Assim $Q_T$ ser invertível é uma condição suficiente para a controlabilidade. veremos que é também necessária.

Se o núcleo $Q_T$ tem um elemento $\mathbf{v} \neq 0$ então $<Q_T\mathbf{v},\mathbf{v}> = \int_0^T ||B^\prime \exp(sA^\prime)\mathbf{v}||^2ds=0$. Pela analiticidade do integrando temos $B^\prime \exp(sA^\prime)\mathbf{v} = 0 \forall s$.

Neste caso temos que para todo controle admissível $u(\cdot)\in \mathcal{U}$

e isto significa que o vetor $\mathbf{v}$ não é acessível pois é ortogonal ao conjunto de atingibilidade de $0$. Portanto para o sistema ser controlável é necessário que a matriz $Q_T$ seja invertível.

[editar] Exercício resolvido

Verificar se é controlável o seguinte sistema:

$Q_{T} = \int_0^T e^{sA}BB'e^{sA'}ds$

$A = \begin{bmatrix} 1 & 0 & -1\\ 0 & 1 & 0\\ 2 & 0 & -1 \end{bmatrix}; A^2 = \begin{bmatrix} -1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & -1 \end{bmatrix}; A^3 = \begin{bmatrix} -1 & 0 & 1\\ 0 & 1 & 0\\ -2 & 0 & 1 \end{bmatrix}; A^4 = I;$

$e^{sA} = I + sA + \frac{s^2 A^2}{2!} + \frac{s^3 A^3}{3!} + ...$

$e^{sA} = \begin{bmatrix} \sin{(s)} + \cos{(s)} & 0 & -\sin{(s)}\\ 0 & e^s & 0\\ 2\sin{(s)} & 0 & -\sin{(s)}+\cos{(s)} \end{bmatrix};$

$e^{sA'} = \begin{bmatrix} \sin{(s)} + \cos{(s)} & 0 & 2\sin{(s)}\\ 0 & e^s & 0\\ -\sin{(s)} & 0 & -\sin{(s)}+\cos{(s)} \end{bmatrix};$

$Q_T = \int_0^T \begin{bmatrix} \sin{(s)} + \cos{(s)} & 0 & -\sin{(s)}\\ 0 & e^s & 0\\ 2\sin{(s)} & 0 & -\sin{(s)}+\cos{(s)} \end{bmatrix} \begin{bmatrix}0 \\ 0 \\ 1 \end{bmatrix} \begin{bmatrix}0 & 0 & 1 \end{bmatrix} \begin{bmatrix} \sin{(s)} + \cos{(s)} & 0 & 2\sin{(s)}\\ 0 & e^s & 0\\ -\sin{(s)} & 0 & -\sin{(s)}+\cos{(s)} \end{bmatrix}ds$

$Q_T = \int_0^T \begin{bmatrix} \sin^2{(s)} & 0 & \sin^2{(s)} - \sin{(s)} . \cos{(s)} \\ 0 & 0 & 0 \\ \sin^2{(s)} - \sin{(s)} . \cos{(s)} & 0 & (\cos{(s)} - \sin{(s)})^2 \end{bmatrix}ds$

[editar] Critério de controlabilidade de Kalman

Definimos o operador linear:

Verifica-se facilmente que o par $(A,B)$ é controlável quando a imagem deste operador linear é o espaço de estados $\mathbb{R}^n$. Como o espaço vetorial $\mathcal{U}$ é de dimensão infinita este operador não tem uma representação matricial. Mas se considerarmos o operador

definido como

com o auxilio do teorema de Cayley-Hamilton podemos mostrar que para qualquer par de matrizes $(A,B)$ as imagens dos operadores $\mathbf{l}_{(A,B)}$ e $\mathcal{L}_T$ coincidem. Neste caso a dimensão da imagem do $\mathbf{l}_{(A,B)}$ é o posto de sua matriz de representação numa base qualquer. Na base canônica a matriz de representação é a matriz de Kalman

Assim o par $(A,B)$ é controlável se e somente se o posto de $\mathbb{K}_{(A,B)}$ for $n$.

[editar] Forma Normal de Kalman, ou decomposição de Kalman.

Suponha que a dimensão da imagem do operador $\mathbf{l}_{(A,B)}$ seja um número $k$ estritamente menor que a dimensão do espaço de estados. Observamos que o subespaço vetorial $V=\text{Im}(\mathbf{l}_{(A,B)})$ é um subespaço invariante por $A$ e que contém a imagem do operador $B$. Escolhendo uma base de $\mathbb{R}^n$ adaptada a este subespaço teremos que nesta nova base o sistema $(A,B)$ terá a forma $(\tilde{A}, \tilde{B})$ com

onde $A_{11} \in \mathbb{R}^{k\times k}$, $A_{12} \in \mathbb{R}^{k\times (n-k)}$, $A_{22} \in \mathbb{R}^{(n-k)\times (n-k)}$ e $B_{1} \in \mathbb{R}^{k\times m}$. Além disso o par $(A_{11},B_1)$ é controlável. Esta é a forma normal de Kalman

É fácil obter as relações

onde $P$ é a matriz de mudança de base da base adaptada para a base canônica. Sempre que tivermos esta relação dizemos que os pares $(A,B)$ e $(\tilde{A},\tilde{B})$ são equivalentes.

[editar] Observabilidade

Retomemos a equação do sistema linear

e verificamos a relação entre as condições iniciais do espaço de estado e a saída do sistema. A questão é: dado o controle admissível podemos identificar o estado inicial do sistema a partir da saída $y(t)$. Diremos que os sistema é observável em tempo $T$ se para quaisquer par de estados $x_a$ e $x_b$ diferentes, as respectivas funções de saída $y_a(t)$ e $y_b(t)$ também diferem. Ou seja: existe $t \in [0,T]$ tal que $y_a(t)-y_b(t)\neq 0$.

Temos que $y_a(t)-y_b(t)=C\exp(tA)(x_a-x_b)$, daí concluímos que o sistema é observável em tempo $T$, ou o par $(A,C)$ é observável, se e somente se, $C\exp(tA)\mathbf{x} \neq 0$ para todo $\mathbf{x}\in\mathbb{R}^n$.

Definimos a matriz de observabilidade :

Então verificamos que

donde o par $(A,C)$ é observável se e somente se $R_T$ for invertível. Como a matriz de observabilidade de $(A,C)$ é exatamente a matriz de controlabilidade de $(A^\prime,C^\prime)$ temos as relações de dualidade. O sistema anterior e observável se e somente se o sistema dual

Analogamente ao caso da controlabilidade podemos escrever os critérios de Kalman para a observabilidade: o par $(A,C)$ é observável quando a matriz de kalman de observabilidade $np\times n$

tem posto máximo.

[editar] Estabilidade de Sistemas Lineares

[editar] matrizes estáveis

Diremos que uma matriz $A \in \mathbb{R}^{n\times n}$ é estável, ou o sistema linear $\dot{x}=Ax$ é estável quando para todo vetor $x \in \mathbb{R}^n$ temos que:

($0$ é assintóticamente estável em EDO)

O conceito de estabilidade não depende das mudanças de base no espaço de estados e se $A$ é estável todas as matrizes equivalentes são estáveis. Para determinar a estabilidade de uma matriz analisamos o conjunto dos autovalores desta matriz.

$$\sigma(A)=\{ \lambda \in \mathbb{C}: \det(A-\lambda \mathbf{I})=0\}$$ é o conjunto dos autovalores de $A$ $$\omega(A)=\sup\{ \text{Re}(\lambda) : \lambda \in \sigma(A) \}$$

A matriz $A$ é estável se e somente se $\omega(A) < 0$

[editar] Polinômios estáveis

Como vimos antes, determinamos a estabilidade de uma matriz $A$ estudando as raizes de seu polinômio característico. De uma forma geral diremos que um polinômio

é estável se todas as raízes deste polinômio têm a parte real negativa. Os polinômios de graus 1 e 2, do tipo acima, são estáveis se e somente se os coeficientes $a_i$ forem todos positivos. Uma condição necessária para que um polinômio geral como o acima (líder=1) seja estável é que todos os coeficientes $a_i$ sejam positivos. Mas esta condição não é mais suficiente se o grau do polinômio for maior que 2.

[editar] Critério de Routh

Dado um polinômio $p(z)$ como acima, com coeficientes reais, e supondo que a condição necessária esteja satisfeita, podemos escrever

Note que se $n$ é par então grau de $U$ é $n$ e grau de $V$ é $n-1$ sendo os líderes dos dois polinômios de sinais opostos.

Se se $n$ é impar então grau de $U$ é $n-1$ e grau de $V$ é $n$ sendo os líderes dos dois polinômios de mesmo sinal.

Construimos agora uma sequência de polinômios $f_1,f_2,\dots , f_k$ da seguinte forma: Se $n$ é par então $f_1(x)=U(x)$ e $f_2(x)=V(x)$; se $n$ for ímpar $f_1(x)=V(x)$ e $f_2(x)=-U(x)$. Os outros termos da sequência são obtidos pela aplicação do algorítmo de Euclides da seguinte forma

a sequência pára quando $f_k(x)=c$.

O critério de Routh diz que o polinômio $p(z)$ é estável se e somente se a sequência $f_1,\dots,f_k$ tem $n+1$ elementos ($k=n+1$) e os sinais dos líderes dos polinômios $f_i$ vão se alternando.

[editar] Matrizes de Routh

O produto de Routh de duas sequências de números reais, $(\alpha_i)_{i\in \mathbb{N}}$, $(\beta_i)_{i\in \mathbb{N}}$ e uma terceira sequência $(\gamma_i)_{i\in \mathbb{N}}$ definida da seguinte forma:

Vamos denotar isso como $\gamma = R(\alpha,\beta)$. Com um polinômio de grau $n$, $p(z)=z^n + a_1 z^{n-1} + \cdots + a_n$, definimos duas sequências

A matriz de Routh de um polinômio, $p$, será uma matrix em que cada linha será uma sequência quase-nula. A primeira linha será a sequência a sequência $\sigma^1$, a segunda será a sequência $\sigma^2$. A $k-$ésima linha será $\sigma^k=R(\sigma^{k-2},\sigma^{k-1})$. Uma variação do critério de Routh acima é:

O polinômio $p(z)$ com todos os coeficientes positivos é estável se e somente se a matriz de Routh tem exatamente $n+1$ linhas 
com o primeiro termo não nulo e todos os termos da primeira coluna são positivos.

[editar] Estabilização de sistemas lineares

Diremos que um par de matrizes $(A,B)$ associado a um sistema linear é estabilizável se existir uma matriz $K\in\mathbb{R}^{m\times n}$ tal que a matriz $A+BK$ fique estável.

Diremos que um par $(A,B)$ é completamente estabilizável quando para qualquer $\omega \in \mathbb{R}$ dado, existe uma matriz $K\in\mathbb{R}^{m\times n}$ tal que $\omega(A+BK)< \omega$

[editar] Um pouco de funções analíticas

[editar] Números complexos

Em primeiro lugar, nos interessa dois aspectos do conjunto dos números complexos: sua característica algébrica de um corpo comutativo completo, e sua característica topológica de um espaço normado

[editar] A estrutura de corpo comutativo

$\mathbb{C}=\{ (a,b)\in \mathbb{R}^2\}$

com as seguintes operações de soma e produto:

1. Soma $$(a,b)+(c,d)=(a+c,b+d)$$
2. Multiplicação $(a,b).(c,d)=(ac-bd,ad+bc)$

Note que a soma é completamente compatível com a estrutura de espaço vetorial de $\mathbb{C}$. Também é fácil verificar as propriedades associativas, comutativas e distributivas das operações. --Patonelli 15h25min de 12 de setembro de 2009 (UTC)

[editar] A estrutura topológica

Uma outra propriedade de $\mathbb{C}$ que vai nos interessar é sua estrutura topológica. Definimos no espaço a norma $|z| = \sqrt{z\bar{z}}$ definindo assim uma topologia compatível com a estrutura de $\mathbb{R}^2$.

[editar] Integração complexa

[editar] Transformada de Laplace