Mudanças entre as edições de "Map2321"
(→Caracterização dos sistemas lineares) |
(→Uma técnica de linearização) |
||
| (21 edições intermediárias de um usuário não apresentadas) | |||
| Linha 72: | Linha 72: | ||
=== Um modelo de economia === | === Um modelo de economia === | ||
| − | Num modelo simples podemos definir as seguintes variáveis | + | Num modelo simples podemos definir as seguintes variáveis, |
| + | |||
<math>Y_n</math> é a receita anual no ano <math>n</math> | <math>Y_n</math> é a receita anual no ano <math>n</math> | ||
<math>C_n</math> total do consumo no ano <math>n</math> | <math>C_n</math> total do consumo no ano <math>n</math> | ||
| Linha 79: | Linha 80: | ||
A equação dinâmica é determinada pelas seguintes relações entre as variáveis | A equação dinâmica é determinada pelas seguintes relações entre as variáveis | ||
| − | {{bluemath|1= | + | {{bluemath| |
| + | 1=<math></math> | ||
# <math>Y_n = C_n + I_n + G_n</math> | # <math>Y_n = C_n + I_n + G_n</math> | ||
# <math>C_n = f(Y_{n-1})</math> O nível de consumo depende da receita do último ano. | # <math>C_n = f(Y_{n-1})</math> O nível de consumo depende da receita do último ano. | ||
| Linha 115: | Linha 117: | ||
Se <math>(x_0,u_0)</math> for um ponto de equilíbrio do campo <math>f(x,u)</math> então o sistema | Se <math>(x_0,u_0)</math> for um ponto de equilíbrio do campo <math>f(x,u)</math> então o sistema | ||
| − | {{ bluemath | <math>\dot{z} = \frac{\partial f}{\partial x}(x_0,u_0)z + \frac{\partial f}{\partial u}(x_0,u_0)v</math> }} | + | {{ bluemath | 1=<math>\dot{z} = \frac{\partial f}{\partial x}(x_0,u_0)z + \frac{\partial f}{\partial u}(x_0,u_0)v</math> }} |
é o sistema linearizado em torno do ponto de equilíbrio. A mesma técnica é utilizada para o ponto de equilíbrio de um sistema discreto. Lembro que o ponto de equilíbrio de um sistema discreto satisfaz <math>f(x_0,u_0)= x_0</math> e do sistema contínuo <math>f(x_0,u_0)= 0</math> | é o sistema linearizado em torno do ponto de equilíbrio. A mesma técnica é utilizada para o ponto de equilíbrio de um sistema discreto. Lembro que o ponto de equilíbrio de um sistema discreto satisfaz <math>f(x_0,u_0)= x_0</math> e do sistema contínuo <math>f(x_0,u_0)= 0</math> | ||
| Linha 129: | Linha 131: | ||
0 & -2\frac{\omega}{r_0} & 0 & 0 \end{pmatrix}(x1x2x3x4)+(00100001)(u1u2)</math> | 0 & -2\frac{\omega}{r_0} & 0 & 0 \end{pmatrix}(x1x2x3x4)+(00100001)(u1u2)</math> | ||
}} | }} | ||
| + | |||
| + | Vamos considerar um segundo exemplo, das equações de Euler de um corpo rígido. As equações são as seguintes: | ||
| + | {{ bluemath | 1= | ||
| + | <math> \begin{gather} | ||
| + | I_1\dot{\omega}_1 = (I_2-I_3)\omega_2 \omega_3 + u_1 \\ | ||
| + | I_2\dot{\omega}_2 = (I_3-I_1)\omega_1 \omega_3 + u_2 \\ | ||
| + | I_3\dot{\omega}_3 = (I_1-I_2)\omega_1 \omega_2 + u_3 \\ | ||
| + | \end{gather} | ||
| + | </math>}} | ||
| + | |||
| + | Vamos considerar <math>I_1=I_2</math> e linearizar o sistema resultante em torno de <math>u_i=0</math> e da trajetória particular | ||
| + | :<math> \begin{gather} | ||
| + | \omega_1(t) = \cos(K\omega_0 t) \\ | ||
| + | \omega_2(t) = \sin(K\omega_0 t) \\ | ||
| + | \omega_3(t) = \omega_0 | ||
| + | \end{gather}</math> | ||
| + | |||
| + | O sistema linearizado, ao longo desta trajetória fica: | ||
| + | {{bluemath|1= | ||
| + | <math>(˙x1˙x2˙x3)= | ||
| + | \begin{pmatrix}0 & -K\omega_0 & -K\sin(K\omega_0 t) \\ | ||
| + | K\omega_0 & 0 & K\cos(K\omega_0t) \\ | ||
| + | 0 & 0 & 0 | ||
| + | \end{pmatrix}(x1x2x3)+(100010001)(u1u2u3)</math> | ||
| + | }} | ||
| + | Neste caso o sistema linear não é invariante no tempo! | ||
== Exponencial de matrizes == | == Exponencial de matrizes == | ||
| + | __MATHJAX__ | ||
Defineremos a exponencial de uma matriz <math>A=(a_{ij})\in \mathbb{R}^{n\times n}</math> como a soma da série: | Defineremos a exponencial de uma matriz <math>A=(a_{ij})\in \mathbb{R}^{n\times n}</math> como a soma da série: | ||
| Linha 137: | Linha 166: | ||
Esta soma converge absolutamente uma vez que introduzimos no espaço das matrizes a [[:en:Matrix_norm#induced_norm | norma induzida]] da norma euclidiana em <math>\mathbb{R}^n</math> | Esta soma converge absolutamente uma vez que introduzimos no espaço das matrizes a [[:en:Matrix_norm#induced_norm | norma induzida]] da norma euclidiana em <math>\mathbb{R}^n</math> | ||
isto é | isto é | ||
| − | {{ bluemath| 1= <math> | + | <math> \newcommand{\norm}[1]{\| #1 \|} </math> |
| + | {{ bluemath| 1= <math> \norm{A} = \sup_{x\neq 0}\{\frac{\norm{Ax}_2}{\norm{x}_2}\}</math>}} | ||
As principais propriedades da exponencial de matrizes: | As principais propriedades da exponencial de matrizes: | ||
| − | {{ bluemath | | + | {{ bluemath | 1= '''Propriedades''' |
# <math>\exp(0)=\mathbf{I}</math> | # <math>\exp(0)=\mathbf{I}</math> | ||
# <math>\exp([\alpha + \beta] A) = \exp(\alpha A)\exp(\beta A)</math> | # <math>\exp([\alpha + \beta] A) = \exp(\alpha A)\exp(\beta A)</math> | ||
| Linha 153: | Linha 183: | ||
:<math>x(t)=\exp(tA)v</math> | :<math>x(t)=\exp(tA)v</math> | ||
é solução da equação diferencial | é solução da equação diferencial | ||
| − | {{ bluemath | | + | {{ bluemath |1= |
<math>\dot{x}=Ax</math>}} | <math>\dot{x}=Ax</math>}} | ||
para que satisfaça também a condição inicial <math>x(t_0)=x_0</math> basta escolher <math>v=\exp(-t_0A)x_0</math> desta forma | para que satisfaça também a condição inicial <math>x(t_0)=x_0</math> basta escolher <math>v=\exp(-t_0A)x_0</math> desta forma | ||
| − | {{ bluemath | <math>x(t) = \exp{(t-t_0)A}x_0</math>}} é solução do problema de Cauchy: | + | {{ bluemath |1= <math>x(t) = \exp{(t-t_0)A}x_0</math>}} é solução do problema de Cauchy: |
| − | {{ bluemath | <math>\dot{x}=Ax</math> | + | {{ bluemath |1= <math>\dot{x}=Ax</math> |
<math>x(t_0)=x_0</math> }} | <math>x(t_0)=x_0</math> }} | ||
Da mesma forma para resolvermos o problema não homogêneo: | Da mesma forma para resolvermos o problema não homogêneo: | ||
| − | {{ bluemath | <math>\dot{x}=Ax+ Bu(t)</math> | + | {{ bluemath |1= <math>\dot{x}=Ax+ Bu(t)</math> |
<math>x(t_0)=x_0</math> }} | <math>x(t_0)=x_0</math> }} | ||
Notemos que a curva | Notemos que a curva | ||
| Linha 172: | Linha 202: | ||
:<math>v(t)=x_0+\int_{t_0}^t\exp(-sA)Bu(s)ds</math> | :<math>v(t)=x_0+\int_{t_0}^t\exp(-sA)Bu(s)ds</math> | ||
e finalmente obtemos a nossa '''aplicação de transição de estados''' | e finalmente obtemos a nossa '''aplicação de transição de estados''' | ||
| − | {{ bluemath | <math>x(t,t_0,x_0,u(\cdot))=\exp((t-t_0)A)x_0+ \int_{t_0}^t \exp([t-s]A)Bu(s)ds</math>}} | + | {{ bluemath | 1= <math>x(t,t_0,x_0,u(\cdot))=\exp((t-t_0)A)x_0+ \int_{t_0}^t \exp([t-s]A)Bu(s)ds</math>}} |
=== Exemplo simples === | === Exemplo simples === | ||
[[Imagem:map2321-orbita1.png|frame|right|Esboço das trajetórias usando controles constantes u=1 e u=-1]] | [[Imagem:map2321-orbita1.png|frame|right|Esboço das trajetórias usando controles constantes u=1 e u=-1]] | ||
O sistema <math>\ddot{\mathbf{x}}=u(t)</math> pode ser escrito como: | O sistema <math>\ddot{\mathbf{x}}=u(t)</math> pode ser escrito como: | ||
| − | {{ bluemath |<math>(˙x˙y) = (0100)(xy)+ (01)u(t) </math>}} | + | {{ bluemath |1=<math>(˙x˙y) = (0100)(xy)+ (01)u(t) </math>}} |
A aplicação da fórmula para a condição inicial no instante <math>t=0</math>, lembrando que <math>\exp(tA)=(1t01)</math>, nos dá | A aplicação da fórmula para a condição inicial no instante <math>t=0</math>, lembrando que <math>\exp(tA)=(1t01)</math>, nos dá | ||
| − | {{ bluemath |<math>(x(t)y(t)) = (x0+y0t+∫t0(t−s)u(s)dsy0+∫t0u(s)ds)</math>}} | + | {{ bluemath |1=<math>(x(t)y(t)) = (x0+y0t+∫t0(t−s)u(s)dsy0+∫t0u(s)ds)</math>}} |
== Controlabilidade == | == Controlabilidade == | ||
| Linha 190: | Linha 220: | ||
A controlabilidade estuda a relação entre os controles e os pontos atingíveis no espaço de estados. Por isso é importante dar algumas propriedades estruturais do conjunto dos controles. Nesta disciplina chamaremos de '''Conjunto dos controles admissíveis''' | A controlabilidade estuda a relação entre os controles e os pontos atingíveis no espaço de estados. Por isso é importante dar algumas propriedades estruturais do conjunto dos controles. Nesta disciplina chamaremos de '''Conjunto dos controles admissíveis''' | ||
o seguinte: | o seguinte: | ||
| − | {{ bluemath | <math>\mathcal{U}= \{ u:\mathbb{R} \to \mathbb{R}^m: \text{ localmente integraveis }\}</math>}} | + | {{ bluemath | 1=<math>\mathcal{U}= \{ u:\mathbb{R} \to \mathbb{R}^m: \text{ localmente integraveis }\}</math>}} |
Este conjunto tem as seguintes propriedades: | Este conjunto tem as seguintes propriedades: | ||
# É um espaço vetorial, | # É um espaço vetorial, | ||
| Linha 200: | Linha 230: | ||
A translação é definida como: | A translação é definida como: | ||
| − | {{ bluemath | <math>\theta_t(u)(s)=u(s-t)</math>}} | + | {{ bluemath |1= <math>\theta_t(u)(s)=u(s-t)</math>}} |
e a concatenação no tempo <math>t_0</math> é definida assim | e a concatenação no tempo <math>t_0</math> é definida assim | ||
| − | {{ bluemath | <math>(u\wedge_{t_0}v)(s) = | + | {{ bluemath | 1=<math>(u\wedge_{t_0}v)(s) = |
\left\{ u(s) se s≤t0v(s) se s>t0\right.</math> | \left\{ u(s) se s≤t0v(s) se s>t0\right.</math> | ||
}} | }} | ||
| Linha 214: | Linha 244: | ||
* <math>\phi(t_1,t_0,x_0,u(\cdot))</math> só depende do valor de <math>u(t)</math> no intervalo <math>[t_0,t_1]</math> | * <math>\phi(t_1,t_0,x_0,u(\cdot))</math> só depende do valor de <math>u(t)</math> no intervalo <math>[t_0,t_1]</math> | ||
No caso dos sistemas lineares independentes do tempo temos | No caso dos sistemas lineares independentes do tempo temos | ||
| − | {{ bluemath |<math>\phi(t,t_0,x_0,u(\cdot))=\exp((t-t_0)A)x_0+ \int_{t_0}^t \exp((t-s)A)Bu(s)ds</math>}} | + | {{ bluemath |1=<math>\phi(t,t_0,x_0,u(\cdot))=\exp((t-t_0)A)x_0+ \int_{t_0}^t \exp((t-s)A)Bu(s)ds</math>}} |
e neste caso temos ainda as seguintes propriedades: | e neste caso temos ainda as seguintes propriedades: | ||
*<math>\phi(t,t_0,x_0,u(\cdot)) =\phi(t,t_0,x_0, 0) + \phi(t_1,t_0,0,u(\cdot)) </math>: decomposição entre dinâmica livre e controlada | *<math>\phi(t,t_0,x_0,u(\cdot)) =\phi(t,t_0,x_0, 0) + \phi(t_1,t_0,0,u(\cdot)) </math>: decomposição entre dinâmica livre e controlada | ||
| Linha 223: | Linha 253: | ||
Se <math>a</math> e <math>b</math> são dois pontos do espaço de estados <math>\mathbb{R}^n</math>, dizemos que <math>b</math> é '''atingível''' em tempo | Se <math>a</math> e <math>b</math> são dois pontos do espaço de estados <math>\mathbb{R}^n</math>, dizemos que <math>b</math> é '''atingível''' em tempo | ||
<math>T</math> a partir de <math>a</math> se existir um controle admissível <math>u(t)\in \mathcal{U}</math> tal que | <math>T</math> a partir de <math>a</math> se existir um controle admissível <math>u(t)\in \mathcal{U}</math> tal que | ||
| − | {{ bluemath | <math>\phi(T,0,a,u(\cdot))=b</math>}} | + | {{ bluemath | 1=<math>\phi(T,0,a,u(\cdot))=b</math>}} |
Nesta caso dizemos também que o controle <math>u</math> transfere <math>a</math> para <math>b</math> em tempo <math>T</math>. O conjunto de todos os pontos atingíveis a partir de <math>a</math> em tempo <math>T>0</math> será denotado por <math>\mathcal{A}(a,T)</math>. | Nesta caso dizemos também que o controle <math>u</math> transfere <math>a</math> para <math>b</math> em tempo <math>T</math>. O conjunto de todos os pontos atingíveis a partir de <math>a</math> em tempo <math>T>0</math> será denotado por <math>\mathcal{A}(a,T)</math>. | ||
No caso do sistema linear é fácil verificar que | No caso do sistema linear é fácil verificar que | ||
| − | {{ bluemath | <math>\mathcal{A}(a,T)= \exp(tA)a + \mathcal{A}(0,T) </math>}} | + | {{ bluemath | 1=<math>\mathcal{A}(a,T)= \exp(tA)a + \mathcal{A}(0,T) </math>}} |
Diremos que o sistema é '''controlável''' quando <math> \mathcal{A}(0,T) = \mathbb{R}^n</math>. | Diremos que o sistema é '''controlável''' quando <math> \mathcal{A}(0,T) = \mathbb{R}^n</math>. | ||
| Linha 235: | Linha 265: | ||
Definiremos a matriz de controlabilidade de <math>(A,B)</math> (ou do sistema ) como | Definiremos a matriz de controlabilidade de <math>(A,B)</math> (ou do sistema ) como | ||
| − | {{ bluemath | <math>Q_T=\int_0^T \exp(sA)BB^\prime \exp(sA^\prime)ds</math>}} | + | {{ bluemath | 1=<math>Q_T=\int_0^T \exp(sA)BB^\prime \exp(sA^\prime)ds</math>}} |
esta matriz é simétrica, semidefinida positiva. Se for definida positiva então é invertível e neste caso o par <math>(A,B)</math> é controlável. | esta matriz é simétrica, semidefinida positiva. Se for definida positiva então é invertível e neste caso o par <math>(A,B)</math> é controlável. | ||
Basta verificar que para qualquer vetor do espaço de estados <math>\mathbf{b} \in \mathbb{R}^n</math> temos que o controle | Basta verificar que para qualquer vetor do espaço de estados <math>\mathbf{b} \in \mathbb{R}^n</math> temos que o controle | ||
| − | {{ bluemath | <math>\hat{u}(s)=B^\prime\exp((T-s)A^\prime)Q_T^{-1}\mathbf{b} </math>}} | + | {{ bluemath |1= <math>\hat{u}(s)=B^\prime\exp((T-s)A^\prime)Q_T^{-1}\mathbf{b} </math>}} |
transfere a origem para <math>\mathbf{b}</math> em tempo <math>T</math> | transfere a origem para <math>\mathbf{b}</math> em tempo <math>T</math> | ||
| Linha 247: | Linha 277: | ||
Neste caso temos que para todo controle admissível <math>u(\cdot)\in \mathcal{U}</math> | Neste caso temos que para todo controle admissível <math>u(\cdot)\in \mathcal{U}</math> | ||
| − | {{ bluemath | <math>\int_0^T <\exp((T-s)A)Bu(s)u(s),\mathbf{v}>ds =0</math>}} | + | {{ bluemath | 1=<math>\int_0^T <\exp((T-s)A)Bu(s)u(s),\mathbf{v}>ds =0</math>}} |
e isto significa que o vetor <math>\mathbf{v}</math> não é acessível pois é ortogonal ao conjunto de atingibilidade de <math>0</math>. Portanto para o sistema ser controlável é necessário que a matriz <math>Q_T</math> seja invertível. | e isto significa que o vetor <math>\mathbf{v}</math> não é acessível pois é ortogonal ao conjunto de atingibilidade de <math>0</math>. Portanto para o sistema ser controlável é necessário que a matriz <math>Q_T</math> seja invertível. | ||
| Linha 253: | Linha 283: | ||
Verificar se é controlável o seguinte sistema: | Verificar se é controlável o seguinte sistema: | ||
| − | {{ bluemath | <math>\dot{[x1x2x3]} = \begin{bmatrix} | + | {{ bluemath | 1= <math>\dot{[x1x2x3] } = \begin{bmatrix} |
1 & 0 & -1\\ | 1 & 0 & -1\\ | ||
0 & 1 & 0\\ | 0 & 1 & 0\\ | ||
| Linha 319: | Linha 349: | ||
\sin^2{(s)} - \sin{(s)} . \cos{(s)} & 0 & (\cos{(s)} - \sin{(s)})^2 \end{bmatrix}ds</math> | \sin^2{(s)} - \sin{(s)} . \cos{(s)} & 0 & (\cos{(s)} - \sin{(s)})^2 \end{bmatrix}ds</math> | ||
| − | {{ bluemath |<math>det{Q_T} = 0 \Rightarrow </math>sistema não é controlável. }} | + | {{ bluemath |1= <math>det{Q_T} = 0 \Rightarrow </math>sistema não é controlável. }} |
=== Critério de controlabilidade de Kalman === | === Critério de controlabilidade de Kalman === | ||
Definimos o operador linear: | Definimos o operador linear: | ||
| − | {{ bluemath |<math>\mathcal{L}_T(u(\cdot))=\int_0^T \exp(sA)Bu(s)ds</math>}} | + | {{ bluemath |1=<math>\mathcal{L}_T(u(\cdot))=\int_0^T \exp(sA)Bu(s)ds</math>}} |
Verifica-se facilmente que o par <math>(A,B)</math> é controlável quando a imagem deste operador linear é o espaço de estados <math>\mathbb{R}^n</math>. | Verifica-se facilmente que o par <math>(A,B)</math> é controlável quando a imagem deste operador linear é o espaço de estados <math>\mathbb{R}^n</math>. | ||
Como o espaço vetorial <math>\mathcal{U}</math> é de dimensão infinita este operador não tem uma representação matricial. | Como o espaço vetorial <math>\mathcal{U}</math> é de dimensão infinita este operador não tem uma representação matricial. | ||
Mas se considerarmos o operador | Mas se considerarmos o operador | ||
| − | {{ bluemath | <math> \mathbf{l}_{(A,B)}: \mathbb{R}^m\times\cdots\times\mathbb{R}^m \to \mathbb{R}^n </math>}} | + | {{ bluemath | 1=<math> \mathbf{l}_{(A,B)}: \mathbb{R}^m\times\cdots\times\mathbb{R}^m \to \mathbb{R}^n </math>}} |
definido como | definido como | ||
| − | {{ bluemath | <math> \mathbf{l}_{(A,B)}(u_0,\dots,u_{n-1})= Bu_0+ABu_1+\cdots + A^{n-1}Bu_{n-1}</math>}} | + | {{ bluemath | 1=<math> \mathbf{l}_{(A,B)}(u_0,\dots,u_{n-1})= Bu_0+ABu_1+\cdots + A^{n-1}Bu_{n-1}</math>}} |
com o auxilio do teorema de [[:en:Cayley_hamilton_theorem | Cayley-Hamilton]] podemos mostrar que para qualquer par de matrizes <math>(A,B)</math> as imagens dos operadores | com o auxilio do teorema de [[:en:Cayley_hamilton_theorem | Cayley-Hamilton]] podemos mostrar que para qualquer par de matrizes <math>(A,B)</math> as imagens dos operadores | ||
<math>\mathbf{l}_{(A,B)} </math> e <math>\mathcal{L}_T </math> coincidem. Neste caso a dimensão da imagem do <math>\mathbf{l}_{(A,B)} </math> é o posto de sua matriz de representação numa base qualquer. Na base canônica a matriz de representação é a '''matriz de Kalman''' | <math>\mathbf{l}_{(A,B)} </math> e <math>\mathcal{L}_T </math> coincidem. Neste caso a dimensão da imagem do <math>\mathbf{l}_{(A,B)} </math> é o posto de sua matriz de representação numa base qualquer. Na base canônica a matriz de representação é a '''matriz de Kalman''' | ||
| − | {{ bluemath | <math>\mathbb{K}_{(A,B)} = [B (AB) \cdots (A^{n-1}B)]\in \mathbb{R}^{n\times nm}</math>}} | + | {{ bluemath |1=<math>\mathbb{K}_{(A,B)} = [B (AB) \cdots (A^{n-1}B)]\in \mathbb{R}^{n\times nm}</math>}} |
Assim o par <math>(A,B)</math> é controlável se e somente se o posto de <math>\mathbb{K}_{(A,B)}</math> for <math>n</math>. | Assim o par <math>(A,B)</math> é controlável se e somente se o posto de <math>\mathbb{K}_{(A,B)}</math> for <math>n</math>. | ||
| Linha 340: | Linha 370: | ||
Suponha que a dimensão da imagem do operador <math>\mathbf{l}_{(A,B)}</math> seja um número <math>k</math> estritamente menor que a dimensão do espaço de estados. Observamos que o subespaço vetorial | Suponha que a dimensão da imagem do operador <math>\mathbf{l}_{(A,B)}</math> seja um número <math>k</math> estritamente menor que a dimensão do espaço de estados. Observamos que o subespaço vetorial | ||
<math>V=\text{Im}(\mathbf{l}_{(A,B)})</math> é um subespaço invariante por <math>A</math> e que contém a imagem do operador <math>B</math>. Escolhendo uma base de <math>\mathbb{R}^n</math> adaptada a este subespaço teremos que nesta nova base o sistema <math>(A,B)</math> terá a forma <math>(\tilde{A}, \tilde{B})</math> com | <math>V=\text{Im}(\mathbf{l}_{(A,B)})</math> é um subespaço invariante por <math>A</math> e que contém a imagem do operador <math>B</math>. Escolhendo uma base de <math>\mathbb{R}^n</math> adaptada a este subespaço teremos que nesta nova base o sistema <math>(A,B)</math> terá a forma <math>(\tilde{A}, \tilde{B})</math> com | ||
| − | {{ bluemath | <math>\tilde{A} = (A11A120A22)</math> | + | {{ bluemath | 1=<math>\tilde{A} = (A11A120A22)</math> |
<math>\tilde{B} = (B10)</math> }} | <math>\tilde{B} = (B10)</math> }} | ||
| Linha 348: | Linha 378: | ||
É fácil obter as relações | É fácil obter as relações | ||
| − | {{ bluemath | <math>\tilde{A} = P^{-1}AP</math> | + | {{ bluemath |1= <math>\tilde{A} = P^{-1}AP</math> |
<math>\tilde{B}=P^{-1}B</math> }} | <math>\tilde{B}=P^{-1}B</math> }} | ||
onde <math>P</math> é a matriz de mudança de base da base adaptada para a base canônica. | onde <math>P</math> é a matriz de mudança de base da base adaptada para a base canônica. | ||
| Linha 356: | Linha 386: | ||
=== Observabilidade === | === Observabilidade === | ||
Retomemos a equação do sistema linear | Retomemos a equação do sistema linear | ||
| − | {{ bluemath |<math>\dot{x}=Ax + Bu</math> | + | {{ bluemath |1=<math>\dot{x}=Ax + Bu</math> |
<math>y=Cx</math>}} | <math>y=Cx</math>}} | ||
e verificamos a relação entre as condições iniciais do espaço de estado e a saída do sistema. | e verificamos a relação entre as condições iniciais do espaço de estado e a saída do sistema. | ||
| Linha 366: | Linha 396: | ||
Definimos a '''matriz de observabilidade ''': | Definimos a '''matriz de observabilidade ''': | ||
| − | {{ bluemath | <math>R_T=\int_0^T \exp(sA^\prime)C^\prime C \exp(sA)ds</math>}} | + | {{ bluemath |1=<math>R_T=\int_0^T \exp(sA^\prime)C^\prime C \exp(sA)ds</math>}} |
Então verificamos que | Então verificamos que | ||
| − | {{ bluemath | <math>\int_0^T | + | {{ bluemath | 1= <math>\int_0^T \norm{C\exp(sA)\mathbf{x} }^2ds= < R_T \mathbf{x},\mathbf{x}></math>}} |
donde o par <math>(A,C)</math> é observável se e somente se <math>R_T</math> for invertível. | donde o par <math>(A,C)</math> é observável se e somente se <math>R_T</math> for invertível. | ||
Como a matriz de observabilidade de <math>(A,C)</math> é exatamente a matriz de controlabilidade de | Como a matriz de observabilidade de <math>(A,C)</math> é exatamente a matriz de controlabilidade de | ||
<math>(A^\prime,C^\prime)</math> temos as relações de dualidade. | <math>(A^\prime,C^\prime)</math> temos as relações de dualidade. | ||
O sistema anterior e observável se e somente se o '''sistema dual''' | O sistema anterior e observável se e somente se o '''sistema dual''' | ||
| − | {{ bluemath |<math>\dot{z} = A^\prime z + C^\prime v</math> | + | {{ bluemath |1=<math>\dot{z} = A^\prime z + C^\prime v</math> |
<math>w=B^\prime z</math>}} for controlável. | <math>w=B^\prime z</math>}} for controlável. | ||
Analogamente ao caso da controlabilidade podemos escrever os critérios de Kalman para a observabilidade: | Analogamente ao caso da controlabilidade podemos escrever os critérios de Kalman para a observabilidade: | ||
o par <math>(A,C)</math> é observável quando a matriz de kalman de observabilidade <math>np\times n</math> | o par <math>(A,C)</math> é observável quando a matriz de kalman de observabilidade <math>np\times n</math> | ||
| − | {{ bluemath | <math>\mathbb{O}_{(A,C)}=[CCA⋮CAn−1]</math>}} | + | {{ bluemath |1= <math>\mathbb{O}_{(A,C)}=[CCA⋮CAn−1]</math>}} |
tem posto máximo. | tem posto máximo. | ||
| Linha 387: | Linha 417: | ||
Diremos que uma matriz <math>A \in \mathbb{R}^{n\times n}</math> é '''estável''', ou o sistema linear <math>\dot{x}=Ax</math> é estável quando | Diremos que uma matriz <math>A \in \mathbb{R}^{n\times n}</math> é '''estável''', ou o sistema linear <math>\dot{x}=Ax</math> é estável quando | ||
para todo vetor <math>x \in \mathbb{R}^n</math> temos que: | para todo vetor <math>x \in \mathbb{R}^n</math> temos que: | ||
| − | {{ bluemath | <math>\lim_{t\to \infty} \exp(tA)x = 0</math>}} | + | {{ bluemath | 1=<math>\lim_{t\to \infty} \exp(tA)x = 0</math>}} |
(<math>0</math> ''é assintóticamente estável em EDO'') | (<math>0</math> ''é assintóticamente estável em EDO'') | ||
| Linha 402: | Linha 432: | ||
Como vimos antes, determinamos a estabilidade de uma matriz <math>A</math> estudando as raizes de seu polinômio característico. De uma forma geral | Como vimos antes, determinamos a estabilidade de uma matriz <math>A</math> estudando as raizes de seu polinômio característico. De uma forma geral | ||
diremos que um polinômio | diremos que um polinômio | ||
| − | {{ bluemath | <math>p(z) = z^n + a_1z^{n-1}+ \cdots + a_n</math> }} | + | {{ bluemath |1= <math>p(z) = z^n + a_1z^{n-1}+ \cdots + a_n</math> }} |
é '''estável''' se todas as raízes deste polinômio têm a parte real negativa. | é '''estável''' se todas as raízes deste polinômio têm a parte real negativa. | ||
Os polinômios de graus 1 e 2, do tipo acima, são estáveis se e somente se os coeficientes <math>a_i</math> forem todos positivos. | Os polinômios de graus 1 e 2, do tipo acima, são estáveis se e somente se os coeficientes <math>a_i</math> forem todos positivos. | ||
| Linha 410: | Linha 440: | ||
Dado um polinômio <math>p(z)</math> como acima, com coeficientes reais, e supondo que a condição necessária esteja satisfeita, podemos escrever | Dado um polinômio <math>p(z)</math> como acima, com coeficientes reais, e supondo que a condição necessária esteja satisfeita, podemos escrever | ||
| − | {{ bluemath | <math>p(\mathbf{i}x) = U(x) + \mathbf{i}V(x)</math> }} | + | {{ bluemath | 1=<math>p(\mathbf{i}x) = U(x) + \mathbf{i}V(x)</math> }} |
Note que se <math>n</math> é par então grau de <math>U</math> é <math>n</math> e grau de <math>V</math> é <math>n-1</math> sendo os líderes dos dois polinômios de sinais opostos. | Note que se <math>n</math> é par então grau de <math>U</math> é <math>n</math> e grau de <math>V</math> é <math>n-1</math> sendo os líderes dos dois polinômios de sinais opostos. | ||
| Linha 417: | Linha 447: | ||
Construimos agora uma sequência de polinômios <math>f_1,f_2,\dots , f_k</math> da seguinte forma: Se <math>n</math> é par então <math>f_1(x)=U(x)</math> | Construimos agora uma sequência de polinômios <math>f_1,f_2,\dots , f_k</math> da seguinte forma: Se <math>n</math> é par então <math>f_1(x)=U(x)</math> | ||
e <math>f_2(x)=V(x)</math>; se <math>n</math> for ímpar <math>f_1(x)=V(x)</math> e <math>f_2(x)=-U(x)</math>. Os outros termos da sequência são obtidos pela aplicação do algorítmo de Euclides da seguinte forma | e <math>f_2(x)=V(x)</math>; se <math>n</math> for ímpar <math>f_1(x)=V(x)</math> e <math>f_2(x)=-U(x)</math>. Os outros termos da sequência são obtidos pela aplicação do algorítmo de Euclides da seguinte forma | ||
| − | {{ bluemath | <math>f_{i-1}(x)= \alpha_i(x)f_{i}(x) - f_{i+1}(x)</math>}} | + | {{ bluemath | 1=<math>f_{i-1}(x)= \alpha_i(x)f_{i}(x) - f_{i+1}(x)</math>}} |
a sequência pára quando <math>f_k(x)=c</math>. | a sequência pára quando <math>f_k(x)=c</math>. | ||
| Linha 425: | Linha 455: | ||
O '''produto de Routh''' de duas sequências de números reais, <math>(\alpha_i)_{i\in \mathbb{N}}</math>, <math>(\beta_i)_{i\in \mathbb{N}}</math> e uma terceira sequência <math>(\gamma_i)_{i\in \mathbb{N}}</math> definida da seguinte forma: | O '''produto de Routh''' de duas sequências de números reais, <math>(\alpha_i)_{i\in \mathbb{N}}</math>, <math>(\beta_i)_{i\in \mathbb{N}}</math> e uma terceira sequência <math>(\gamma_i)_{i\in \mathbb{N}}</math> definida da seguinte forma: | ||
| − | {{ bluemath | <math>\gamma_k=\frac{-1}{\beta_1}\ | + | {{ bluemath | 1=<math>\gamma_k=\frac{-1}{\beta_1}\text{det} \begin{bmatrix} \alpha_1 & \alpha_{k+1} \\ \beta_1 & \beta_{k+1}\end{bmatrix}</math>}} |
Vamos denotar isso como <math>\gamma = R(\alpha,\beta)</math>. Com um polinômio de grau <math>n</math>, <math>p(z)=z^n + a_1 z^{n-1} + \cdots + a_n</math>, definimos duas sequências | Vamos denotar isso como <math>\gamma = R(\alpha,\beta)</math>. Com um polinômio de grau <math>n</math>, <math>p(z)=z^n + a_1 z^{n-1} + \cdots + a_n</math>, definimos duas sequências | ||
| − | {{ bluemath | <math>\sigma^1: 1, a_2, a_4, \dots , 0, 0, \dots</math> | + | {{ bluemath |1= <math>\sigma^1: 1, a_2, a_4, \dots , 0, 0, \dots</math> |
<math>\sigma^2: a_1, a_3, \dots, 0, 0, \dots</math>}} | <math>\sigma^2: a_1, a_3, \dots, 0, 0, \dots</math>}} | ||
A matriz de Routh de um polinômio, <math>p</math>, será uma matrix em que cada linha será uma sequência quase-nula. A primeira linha será a sequência | A matriz de Routh de um polinômio, <math>p</math>, será uma matrix em que cada linha será uma sequência quase-nula. A primeira linha será a sequência | ||
| Linha 441: | Linha 471: | ||
<math>K\in\mathbb{R}^{m\times n}</math> tal que <math>\omega(A+BK)< \omega</math> | <math>K\in\mathbb{R}^{m\times n}</math> tal que <math>\omega(A+BK)< \omega</math> | ||
| − | {{ bluemath | São equivalentes | + | {{ bluemath | 1= São equivalentes |
# <math>(A,B)</math> é completamente estabilizável. | # <math>(A,B)</math> é completamente estabilizável. | ||
# <math>(A,B)</math> é controlável. | # <math>(A,B)</math> é controlável. | ||
Edição atual tal como às 18h10min de 14 de agosto de 2013
| Se você quiser editar leia as Dicas de formatação deste wiki, e mãos à obra!. |
[editar] Aspectos históricos da teoria de Controle
Em praticamente todos os sistemas da natureza há a possibilidade de intervenção que permite exercer algum controle sobre o sistema. Aspectos tecnológicos nos fazem procurar uma forma de exercer este controle automaticamente. É o que chamaremos de retroalimentação do sistema.
Basicamente a origem da teoria de controle são os sistemas de regulagem, isto é, procura-se desenvolver um processo automático para que um sistema fique numa situação de equilíbrio. Assim um sensor detecta se o sistema está se desregulando e um controlador atuaria automaticamente para restabelecer o equilibrio. Claro que muitos mecanismos engenhosos foram desenvolvidos durante milênios para resolver este problema, porém um caso interessante era o de controle de velocidade de moinhos de vento. Huygens inventou um instrumento conhecido como flyball que na pratica resolvia o problema. Esta mesma idéia do flyball foi usada depois por Watt em máquinas para o controle de fluxo de vapor. Este modelo que funcionava na prática tinha um problema de excesso de vibração para velocidades muito altas. Foi Maxwell quem elaborou um modelo matemático para o flyball e colocou o problema de eliminação das vibrações como um problema de estabilização. Este foi, pode-se dizer, o primeiro problema matemático da teoria de controle.
No começo do século XX, o desenvolvimento das redes de comunicações telefônicas, propiciou o aparecimento de novos modelos e a utilização de métodos da teoria de funções a variáveis complexas para eliminação de ruídos e filtragens de sinais. Os trabalhos pioneiros nesta linha deveu-se a Black, Bode e Nyquist do grupo do laboratório Bell. O conjunto de métodos desenvolvidos por eles influenciou bastante a engenharia e é chamado de teoria de controle clássica. Isso foi mais ou menos em 1930. Depois da segunda guerra mundial os métodos de otimização ganharam importância e é um mérito da teoria de Pontriaguin o estudo da teoria de controle ótimo. O desenvolvimento da teoria de sistemas dinâmicos propiciou uma nova abordagem para os sistemas de controles lineares. Assim nas décadas de 1960 e 1970 desenvolveu-se bastante uma teoria estrutural dos sistemas de controle. E nesta abordagem "moderna" baseada no espaço de estados dos sistemas são importantes os conceitos de controlabilidade e observabilidade introduzidos por Kalman. No final do século passado desenvolveram-se os métodos geometricos para o estudo de sistema de controle não linear. Em todos estes tópicos há ainda pesquisa bastante ativa. --Patonelli 15h27min de 24 de agosto de 2009 (UTC)patonelli
[editar] Exemplos de sistemas de controle
[editar] Um satélite simples num campo newtoniano
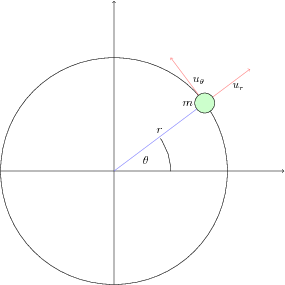
Uma partícula de massa m está sob ação de um campo de acelerações central newtoniano. Além disso podemos colocar dois controles independentes, um na direção radial e outro na direção tangencial ur e uθ respectivamente. A equação dinâmica deste sistema é dada pela segunda lei de Newton:
| m¨r=(−kr2+ur)er+uθeθ |
fazendo a massa m=1 para que eu não tenha que ficar digitando coisas a mais. Podemos reecrever as equações em coordenadas polares como:
| ¨r=r˙θ2−kr2+ur r¨θ=−2˙r˙θ+uθ |
Estas duas equações nos dão um sistema de controle não linear com duas entradas de controle. Voltaremos a este exemplo quando falarmos de linearização.
--Patonelli 21h10min de 22 de agosto de 2009 (UTC)patonelli
[editar] O pêndulo invertido
O pêndulo invertido é um problema clássico em teoria de controle, as equações do movimento são:
| (M+m)¨x−ml¨θcosθ+ml˙θ2sinθ=F
ml(−gsinθ−¨xcosθ+l¨θ)=0 |
A variável de controle aqui é a força F
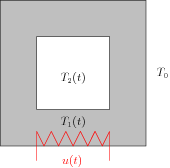
[editar] Um forno simplificado
A figura mostra o esquema de um forno constituído de uma jaqueta de um material (a parte cinza) que é aquecido por uma resistência, e o calor é transmitido para o interior do forno. A taxa de calor u(t) é o controle do sistema. As temperaturas (que estamos supondo ser uniformemente distribuídas no espaçao!) T1(t) e T2(t) são as variáveis de estados. Sendo c1 e c2 as capacidades térmicas da jaqueta e do interior do forno respectivamente; a1 e a2 área exterior e interior da jaqueta; r1 e r2 os coeficientes de transmissão de calor da parte externa e interna da jaqueta e T0 a temperatura exterior. A equação de balanço térmico nos dá:
| c1˙x1(t)=(−r2a2−r1a1)x1+r2a2x2+u(t)
c2˙x2(t)=r2a2x1−r2a2x2 |
Onde x1=T1−T0 e x2=T2−T0
[editar] Um circuito elétrico
Na figura ao lado vemos as equações dinâmicas de alguns componentes elétricos: resistores, condensadores e indutores. Usaremos estas equações e as leis de Kirchoff dos nós e das malhas para escrever a relação dinâmica entre voltagem e corrente do circuito abaixo.
Chamaremos de x1 a voltagem pelo capacitor C do circuito, e de x2 a corrente através do indutor L Aplicando as leis constitutivas dos elementos e as leis de Kirchoff temos as relações dinâmicas
| ˙x1=−x1R1C+vR1C ˙x2=−x2R2L+vL |
Neste caso v(t) é a única entrada do sistema (e portanto o controle) e a corrente é a saída do sistema. Para encontrar a relação entre entrada e saída temos resolver uma equação diferencial nas variáveis x1 e x2, que podem ser interpretadas como variáveis auxiliares neste caso. --Patonelli 21h32min de 22 de agosto de 2009 (UTC)patonelli
[editar] Um modelo de economia
Num modelo simples podemos definir as seguintes variáveis,
Yn é a receita anual no ano n Cn total do consumo no ano n In investimento no ano Gn gastos do governo
A equação dinâmica é determinada pelas seguintes relações entre as variáveis
|
O controle do sistema é Gn. A equação a diferenças finitas fica
| Yn=f(Yn−1)+g(f(Yn−1)−f(Yn−2))+Gn |
--Patonelli 23h04min de 22 de agosto de 2009 (UTC)patonelli
[editar] Caracterização dos sistemas lineares
Os exemplos acima nos dão as principais carecterísticas dos sistemas de controle. Dependendo do sistema ser contínuo ou discreto temos as equações
| ˙x(t)=f(x(t),u(t)) y(t)=g(x(t),u(t)) |
e no caso discreto
| xn+1=f(xn,un) yn=g(xn,un) |
onde x∈Rn é a variável de estado, y∈Rp é a variável de saída e u∈Rm são os parâmetros de entrada.
As funções estruturais do sistema f:Rn×Rm→Rn e g:Rn×Rm→Rp são usadas para classificar os sistemas. No nosso caso estaremos interessado somente nos casos de sistemas lineares invariantes no tempo, ou seja quando
| f(x,u)=Ax+Bu g(x,u)=Cx |
Com A matriz n×n, B matriz n×m e C matriz p×n. Nas próximas sessões vamos analisar mais detalhadamente estes exemplos.
[editar] Uma técnica de linearização
Se (x0,u0) for um ponto de equilíbrio do campo f(x,u) então o sistema
| ˙z=∂f∂x(x0,u0)z+∂f∂u(x0,u0)v |
é o sistema linearizado em torno do ponto de equilíbrio. A mesma técnica é utilizada para o ponto de equilíbrio de um sistema discreto. Lembro que o ponto de equilíbrio de um sistema discreto satisfaz f(x0,u0)=x0 e do sistema contínuo f(x0,u0)=0
Como exemplo retomamos a equação do satélite. fazendo uθ=ur=0, encontramos um movimento circular uniforme que é uma trajetória de equilíbrio para um determinado momento angularr(t)=r0,θ(t)=ωt Agora fazemos as mudanças de variáveis:
| x1=r(t)−r0,x2=˙x1,x3=θ(t)−ωt,x4=˙x3 |
e usando a técnica de linearização ensinada obtemos os sistema linear:
| (˙x1˙x2˙x3˙x4)=(01003ω2002ωr000010−2ωr000)(x1x2x3x4)+(00100001)(u1u2) |
Vamos considerar um segundo exemplo, das equações de Euler de um corpo rígido. As equações são as seguintes:
| I1˙ω1=(I2−I3)ω2ω3+u1I2˙ω2=(I3−I1)ω1ω3+u2I3˙ω3=(I1−I2)ω1ω2+u3 |
Vamos considerar I1=I2 e linearizar o sistema resultante em torno de ui=0 e da trajetória particular ω1(t)=cos(Kω0t)ω2(t)=sin(Kω0t)ω3(t)=ω0
O sistema linearizado, ao longo desta trajetória fica:
| (˙x1˙x2˙x3)=(0−Kω0−Ksin(Kω0t)Kω00Kcos(Kω0t)000)(x1x2x3)+(100010001)(u1u2u3) |
Neste caso o sistema linear não é invariante no tempo!
[editar] Exponencial de matrizes
Defineremos a exponencial de uma matriz A=(aij)∈Rn×n como a soma da série:
| exp(A)=∑∞k=0Akk! |
Esta soma converge absolutamente uma vez que introduzimos no espaço das matrizes a norma induzida da norma euclidiana em Rn isto é \newcommand{\norm}[1]{\| #1 \|}
| \norm{A} = \sup_{x\neq 0}\{\frac{\norm{Ax}_2}{\norm{x}_2}\} |
As principais propriedades da exponencial de matrizes:
Propriedades
|
[editar] Solução das equações lineares não homegêneas
Em primeiro lugar note que pela propriedade 6 acima a curva x(t)=\exp(tA)v é solução da equação diferencial
| \dot{x}=Ax |
para que satisfaça também a condição inicial x(t_0)=x_0 basta escolher v=\exp(-t_0A)x_0 desta forma
| x(t) = \exp{(t-t_0)A}x_0 |
| \dot{x}=Ax
x(t_0)=x_0 |
Da mesma forma para resolvermos o problema não homogêneo:
| \dot{x}=Ax+ Bu(t)
x(t_0)=x_0 |
Notemos que a curva x(t)=\exp(tA)v(t) satisfaz a equação: \dot{x}=Ax + \exp(tA)\dot{v}(t) Resolvendo a equação em v(t) \exp(tA)\dot{v}(t)=Bu(t) \exp(t_0A)v(t_0)=x_0 obtemos v(t)=x_0+\int_{t_0}^t\exp(-sA)Bu(s)ds e finalmente obtemos a nossa aplicação de transição de estados
| x(t,t_0,x_0,u(\cdot))=\exp((t-t_0)A)x_0+ \int_{t_0}^t \exp([t-s]A)Bu(s)ds |
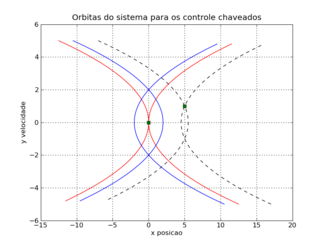
[editar] Exemplo simples
O sistema \ddot{\mathbf{x}}=u(t) pode ser escrito como:
| \begin{pmatrix} \dot{x} \\ \dot{y}\end{pmatrix} = \begin{pmatrix}0 & 1 \\ 0 & 0 \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}+ \begin{pmatrix}0 \\ 1 \end{pmatrix}u(t) |
A aplicação da fórmula para a condição inicial no instante t=0, lembrando que \exp(tA)=\begin{pmatrix} 1 & t \\ 0 & 1 \end{pmatrix}, nos dá
| \begin{pmatrix} x(t) \\ y(t) \end{pmatrix} = \begin{pmatrix} x_0 + y_0t + \int_0^t (t-s)u(s)ds \\ y_0 + \int_0^t u(s)ds \end{pmatrix} |
[editar] Controlabilidade
Antes de abordar controlabilidade convém falar de dois tópicos:
[editar] Controles admissíveis
A controlabilidade estuda a relação entre os controles e os pontos atingíveis no espaço de estados. Por isso é importante dar algumas propriedades estruturais do conjunto dos controles. Nesta disciplina chamaremos de Conjunto dos controles admissíveis o seguinte:
| \mathcal{U}= \{ u:\mathbb{R} \to \mathbb{R}^m: \text{ localmente integraveis }\} |
Este conjunto tem as seguintes propriedades:
- É um espaço vetorial,
- É invariante pelo sistema dinâmico de translação \theta_t
- É fechado pela concatenação \wedge_{t_0} para todo t_0\in \mathbb{R}
- Contém a família das funções constantes por partes
Um subconjunto de \mathcal{U} com estas quatro propriedades também pode ser chamado de um conjunto de controles admissíveis e alteraria um pouco o estudo da controlabilidade. Este conjunto que vamos usar pode ser pensado como o maior conjunto de controles admissíveis.
A translação é definida como:
| \theta_t(u)(s)=u(s-t) |
e a concatenação no tempo t_0 é definida assim
| (u\wedge_{t_0}v)(s) = \left\{ \begin{array}{cl} u(s) & \text{ se } s\leq t_0 \\ v(s) & \text{ se } s > t_0 \end{array}\right. |
[editar] Propriedades da aplicação de transição de estados
Para os sistemas de controle contínuos de forma geral, aplicação de transição de estados é uma aplicação:
| \phi: \mathbb{R} \times \mathbb{R}\times \mathbb{R}^n \times \mathcal{U} \to \mathbb{R}^n |
Satisfazendo as propriedades:
- \phi(t,t,x_0,u(\cdot))=x_0, chamada de compatibilidade.
- \phi(t_2, t_1, \phi(t_1,t_0,x_0,u(\cdot)),v(\cdot))=\phi(t_2,t_0,x_0,u\wedge_{t_1}v(\cdot)), sistema dinâmico.
- \phi(t_1,t_0,x_0,u(\cdot)) só depende do valor de u(t) no intervalo [t_0,t_1]
No caso dos sistemas lineares independentes do tempo temos
| \phi(t,t_0,x_0,u(\cdot))=\exp((t-t_0)A)x_0+ \int_{t_0}^t \exp((t-s)A)Bu(s)ds |
e neste caso temos ainda as seguintes propriedades:
- \phi(t,t_0,x_0,u(\cdot)) =\phi(t,t_0,x_0, 0) + \phi(t_1,t_0,0,u(\cdot)) : decomposição entre dinâmica livre e controlada
- \phi(t,t_0,x_0 + x_1,u(\cdot)+ v(\cdot)) = \phi(t,t_0,x_0,u(\cdot))+ \phi(t,t_0,x_1,v(\cdot)) : princípio da superposição
- \phi(t,t_0,x_0,\theta_{t_0}u(\cdot))= \phi(t-t_0,0,x_0,u(\cdot)) : invariante no tempo.
Esta última propriedade é que nos justifica o estudo da controlabilidade só quando o tempo inicial é 0
Se a e b são dois pontos do espaço de estados \mathbb{R}^n, dizemos que b é atingível em tempo T a partir de a se existir um controle admissível u(t)\in \mathcal{U} tal que
| \phi(T,0,a,u(\cdot))=b |
Nesta caso dizemos também que o controle u transfere a para b em tempo T. O conjunto de todos os pontos atingíveis a partir de a em tempo T>0 será denotado por \mathcal{A}(a,T).
No caso do sistema linear é fácil verificar que
| \mathcal{A}(a,T)= \exp(tA)a + \mathcal{A}(0,T) |
Diremos que o sistema é controlável quando \mathcal{A}(0,T) = \mathbb{R}^n.
[editar] Matriz de controlabilidade
Note que o conjunto \mathcal{A}(0,T) depende apenas das matrizes A, B do tempo T>0 e da família de controles admissíveis. Quando o sistema for controlável diremos que o par (A,B) é controlável.
Definiremos a matriz de controlabilidade de (A,B) (ou do sistema ) como
| Q_T=\int_0^T \exp(sA)BB^\prime \exp(sA^\prime)ds |
esta matriz é simétrica, semidefinida positiva. Se for definida positiva então é invertível e neste caso o par (A,B) é controlável.
Basta verificar que para qualquer vetor do espaço de estados \mathbf{b} \in \mathbb{R}^n temos que o controle
| \hat{u}(s)=B^\prime\exp((T-s)A^\prime)Q_T^{-1}\mathbf{b} |
transfere a origem para \mathbf{b} em tempo T
Assim Q_T ser invertível é uma condição suficiente para a controlabilidade. veremos que é também necessária.
Se o núcleo Q_T tem um elemento \mathbf{v} \neq 0 então <Q_T\mathbf{v},\mathbf{v}> = \int_0^T ||B^\prime \exp(sA^\prime)\mathbf{v}||^2ds=0. Pela analiticidade do integrando temos B^\prime \exp(sA^\prime)\mathbf{v} = 0 \forall s .
Neste caso temos que para todo controle admissível u(\cdot)\in \mathcal{U}
| \int_0^T <\exp((T-s)A)Bu(s)u(s),\mathbf{v}>ds =0 |
e isto significa que o vetor \mathbf{v} não é acessível pois é ortogonal ao conjunto de atingibilidade de 0. Portanto para o sistema ser controlável é necessário que a matriz Q_T seja invertível.
[editar] Exercício resolvido
Verificar se é controlável o seguinte sistema:
| \dot{\begin{bmatrix}x_1 \\ x_2 \\ x_3 \end{bmatrix} } = \begin{bmatrix} 1 & 0 & -1\\ 0 & 1 & 0\\ 2 & 0 & -1 \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3 \end{bmatrix} + \begin{bmatrix} 0\\ 0\\ 1 \end{bmatrix}u |
Q_{T} = \int_0^T e^{sA}BB'e^{sA'}ds
A = \begin{bmatrix} 1 & 0 & -1\\ 0 & 1 & 0\\ 2 & 0 & -1 \end{bmatrix}; A^2 = \begin{bmatrix} -1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & -1 \end{bmatrix}; A^3 = \begin{bmatrix} -1 & 0 & 1\\ 0 & 1 & 0\\ -2 & 0 & 1 \end{bmatrix}; A^4 = I;
e^{sA} = I + sA + \frac{s^2 A^2}{2!} + \frac{s^3 A^3}{3!} + ...
e^{sA} = \begin{bmatrix} \sin{(s)} + \cos{(s)} & 0 & -\sin{(s)}\\ 0 & e^s & 0\\ 2\sin{(s)} & 0 & -\sin{(s)}+\cos{(s)} \end{bmatrix};
e^{sA'} = \begin{bmatrix} \sin{(s)} + \cos{(s)} & 0 & 2\sin{(s)}\\ 0 & e^s & 0\\ -\sin{(s)} & 0 & -\sin{(s)}+\cos{(s)} \end{bmatrix};
Q_T = \int_0^T \begin{bmatrix} \sin{(s)} + \cos{(s)} & 0 & -\sin{(s)}\\ 0 & e^s & 0\\ 2\sin{(s)} & 0 & -\sin{(s)}+\cos{(s)} \end{bmatrix} \begin{bmatrix}0 \\ 0 \\ 1 \end{bmatrix} \begin{bmatrix}0 & 0 & 1 \end{bmatrix} \begin{bmatrix} \sin{(s)} + \cos{(s)} & 0 & 2\sin{(s)}\\ 0 & e^s & 0\\ -\sin{(s)} & 0 & -\sin{(s)}+\cos{(s)} \end{bmatrix}ds
Q_T = \int_0^T \begin{bmatrix} \sin^2{(s)} & 0 & \sin^2{(s)} - \sin{(s)} . \cos{(s)} \\ 0 & 0 & 0 \\ \sin^2{(s)} - \sin{(s)} . \cos{(s)} & 0 & (\cos{(s)} - \sin{(s)})^2 \end{bmatrix}ds
| det{Q_T} = 0 \Rightarrow sistema não é controlável. |
[editar] Critério de controlabilidade de Kalman
Definimos o operador linear:
| \mathcal{L}_T(u(\cdot))=\int_0^T \exp(sA)Bu(s)ds |
Verifica-se facilmente que o par (A,B) é controlável quando a imagem deste operador linear é o espaço de estados \mathbb{R}^n. Como o espaço vetorial \mathcal{U} é de dimensão infinita este operador não tem uma representação matricial. Mas se considerarmos o operador
| \mathbf{l}_{(A,B)}: \mathbb{R}^m\times\cdots\times\mathbb{R}^m \to \mathbb{R}^n |
definido como
| \mathbf{l}_{(A,B)}(u_0,\dots,u_{n-1})= Bu_0+ABu_1+\cdots + A^{n-1}Bu_{n-1} |
com o auxilio do teorema de Cayley-Hamilton podemos mostrar que para qualquer par de matrizes (A,B) as imagens dos operadores \mathbf{l}_{(A,B)} e \mathcal{L}_T coincidem. Neste caso a dimensão da imagem do \mathbf{l}_{(A,B)} é o posto de sua matriz de representação numa base qualquer. Na base canônica a matriz de representação é a matriz de Kalman
| \mathbb{K}_{(A,B)} = [B (AB) \cdots (A^{n-1}B)]\in \mathbb{R}^{n\times nm} |
Assim o par (A,B) é controlável se e somente se o posto de \mathbb{K}_{(A,B)} for n.
[editar] Forma Normal de Kalman, ou decomposição de Kalman.
Suponha que a dimensão da imagem do operador \mathbf{l}_{(A,B)} seja um número k estritamente menor que a dimensão do espaço de estados. Observamos que o subespaço vetorial V=\text{Im}(\mathbf{l}_{(A,B)}) é um subespaço invariante por A e que contém a imagem do operador B. Escolhendo uma base de \mathbb{R}^n adaptada a este subespaço teremos que nesta nova base o sistema (A,B) terá a forma (\tilde{A}, \tilde{B}) com
| \tilde{A} = \begin{pmatrix}A_{11} & A_{12} \\ \mathbf{0} & A_{22} \end{pmatrix}
\tilde{B} = \begin{pmatrix}B_1 \\ 0 \end{pmatrix} |
onde A_{11} \in \mathbb{R}^{k\times k}, A_{12} \in \mathbb{R}^{k\times (n-k)}, A_{22} \in \mathbb{R}^{(n-k)\times (n-k)} e B_{1} \in \mathbb{R}^{k\times m} . Além disso o par (A_{11},B_1) é controlável. Esta é a forma normal de Kalman
É fácil obter as relações
| \tilde{A} = P^{-1}AP
\tilde{B}=P^{-1}B |
onde P é a matriz de mudança de base da base adaptada para a base canônica. Sempre que tivermos esta relação dizemos que os pares (A,B) e (\tilde{A},\tilde{B}) são equivalentes.
[editar] Observabilidade
Retomemos a equação do sistema linear
| \dot{x}=Ax + Bu
y=Cx |
e verificamos a relação entre as condições iniciais do espaço de estado e a saída do sistema. A questão é: dado o controle admissível podemos identificar o estado inicial do sistema a partir da saída y(t). Diremos que os sistema é observável em tempo T se para quaisquer par de estados x_a e x_b diferentes, as respectivas funções de saída y_a(t) e y_b(t) também diferem. Ou seja: existe t \in [0,T] tal que y_a(t)-y_b(t)\neq 0.
Temos que y_a(t)-y_b(t)=C\exp(tA)(x_a-x_b), daí concluímos que o sistema é observável em tempo T, ou o par (A,C) é observável, se e somente se, C\exp(tA)\mathbf{x} \neq 0 para todo \mathbf{x}\in\mathbb{R}^n.
Definimos a matriz de observabilidade :
| R_T=\int_0^T \exp(sA^\prime)C^\prime C \exp(sA)ds |
Então verificamos que
| \int_0^T \norm{C\exp(sA)\mathbf{x} }^2ds= < R_T \mathbf{x},\mathbf{x}> |
donde o par (A,C) é observável se e somente se R_T for invertível. Como a matriz de observabilidade de (A,C) é exatamente a matriz de controlabilidade de (A^\prime,C^\prime) temos as relações de dualidade. O sistema anterior e observável se e somente se o sistema dual
| \dot{z} = A^\prime z + C^\prime v
w=B^\prime z |
Analogamente ao caso da controlabilidade podemos escrever os critérios de Kalman para a observabilidade: o par (A,C) é observável quando a matriz de kalman de observabilidade np\times n
| \mathbb{O}_{(A,C)}=\begin{bmatrix} C \\ CA \\ \vdots \\ CA^{n-1}\end{bmatrix} |
tem posto máximo.
[editar] Estabilidade de Sistemas Lineares
[editar] matrizes estáveis
Diremos que uma matriz A \in \mathbb{R}^{n\times n} é estável, ou o sistema linear \dot{x}=Ax é estável quando para todo vetor x \in \mathbb{R}^n temos que:
| \lim_{t\to \infty} \exp(tA)x = 0 |
(0 é assintóticamente estável em EDO)
O conceito de estabilidade não depende das mudanças de base no espaço de estados e se A é estável todas as matrizes equivalentes são estáveis. Para determinar a estabilidade de uma matriz analisamos o conjunto dos autovalores desta matriz.
\sigma(A)=\{ \lambda \in \mathbb{C}: \det(A-\lambda \mathbf{I})=0\} é o conjunto dos autovalores de A \omega(A)=\sup\{ \text{Re}(\lambda) : \lambda \in \sigma(A) \}
A matriz A é estável se e somente se \omega(A) < 0
[editar] Polinômios estáveis
Como vimos antes, determinamos a estabilidade de uma matriz A estudando as raizes de seu polinômio característico. De uma forma geral diremos que um polinômio
| p(z) = z^n + a_1z^{n-1}+ \cdots + a_n |
é estável se todas as raízes deste polinômio têm a parte real negativa. Os polinômios de graus 1 e 2, do tipo acima, são estáveis se e somente se os coeficientes a_i forem todos positivos. Uma condição necessária para que um polinômio geral como o acima (líder=1) seja estável é que todos os coeficientes a_i sejam positivos. Mas esta condição não é mais suficiente se o grau do polinômio for maior que 2.
[editar] Critério de Routh
Dado um polinômio p(z) como acima, com coeficientes reais, e supondo que a condição necessária esteja satisfeita, podemos escrever
| p(\mathbf{i}x) = U(x) + \mathbf{i}V(x) |
Note que se n é par então grau de U é n e grau de V é n-1 sendo os líderes dos dois polinômios de sinais opostos.
Se se n é impar então grau de U é n-1 e grau de V é n sendo os líderes dos dois polinômios de mesmo sinal.
Construimos agora uma sequência de polinômios f_1,f_2,\dots , f_k da seguinte forma: Se n é par então f_1(x)=U(x) e f_2(x)=V(x); se n for ímpar f_1(x)=V(x) e f_2(x)=-U(x). Os outros termos da sequência são obtidos pela aplicação do algorítmo de Euclides da seguinte forma
| f_{i-1}(x)= \alpha_i(x)f_{i}(x) - f_{i+1}(x) |
a sequência pára quando f_k(x)=c.
O critério de Routh diz que o polinômio p(z) é estável se e somente se a sequência f_1,\dots,f_k tem n+1 elementos (k=n+1) e os sinais dos líderes dos polinômios f_i vão se alternando.
[editar] Matrizes de Routh
O produto de Routh de duas sequências de números reais, (\alpha_i)_{i\in \mathbb{N}}, (\beta_i)_{i\in \mathbb{N}} e uma terceira sequência (\gamma_i)_{i\in \mathbb{N}} definida da seguinte forma:
| \gamma_k=\frac{-1}{\beta_1}\text{det} \begin{bmatrix} \alpha_1 & \alpha_{k+1} \\ \beta_1 & \beta_{k+1}\end{bmatrix} |
Vamos denotar isso como \gamma = R(\alpha,\beta). Com um polinômio de grau n, p(z)=z^n + a_1 z^{n-1} + \cdots + a_n, definimos duas sequências
| \sigma^1: 1, a_2, a_4, \dots , 0, 0, \dots
\sigma^2: a_1, a_3, \dots, 0, 0, \dots |
A matriz de Routh de um polinômio, p, será uma matrix em que cada linha será uma sequência quase-nula. A primeira linha será a sequência a sequência \sigma^1, a segunda será a sequência \sigma^2. A k-ésima linha será \sigma^k=R(\sigma^{k-2},\sigma^{k-1}). Uma variação do critério de Routh acima é:
O polinômio p(z) com todos os coeficientes positivos é estável se e somente se a matriz de Routh tem exatamente n+1 linhas com o primeiro termo não nulo e todos os termos da primeira coluna são positivos.
[editar] Estabilização de sistemas lineares
Diremos que um par de matrizes (A,B) associado a um sistema linear é estabilizável se existir uma matriz K\in\mathbb{R}^{m\times n} tal que a matriz A+BK fique estável.
Diremos que um par (A,B) é completamente estabilizável quando para qualquer \omega \in \mathbb{R} dado, existe uma matriz K\in\mathbb{R}^{m\times n} tal que \omega(A+BK)< \omega
São equivalentes
|
[editar] Um pouco de funções analíticas
[editar] Números complexos
Em primeiro lugar, nos interessa dois aspectos do conjunto dos números complexos: sua característica algébrica de um corpo comutativo completo, e sua característica topológica de um espaço normado
[editar] A estrutura de corpo comutativo
\mathbb{C}=\{ (a,b)\in \mathbb{R}^2\}
com as seguintes operações de soma e produto:
- Soma (a,b)+(c,d)=(a+c,b+d)
- Multiplicação (a,b).(c,d)=(ac-bd,ad+bc)
Note que a soma é completamente compatível com a estrutura de espaço vetorial de \mathbb{C} . Também é fácil verificar as propriedades associativas, comutativas e distributivas das operações.
--Patonelli 15h25min de 12 de setembro de 2009 (UTC)
[editar] A estrutura topológica
Uma outra propriedade de \mathbb{C} que vai nos interessar é sua estrutura topológica. Definimos no espaço a norma |z| = \sqrt{z\bar{z}} definindo assim uma topologia compatível com a estrutura de \mathbb{R}^2.