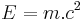Mudanças entre as edições de "Teced/textos/grupo32"
(→Leis de Newton) |
(→Bibliografia) |
||
| (7 edições intermediárias de 3 usuários não apresentadas) | |||
| Linha 6: | Linha 6: | ||
== Introdução == | == Introdução == | ||
| − | A ciência da física mecânica surge com uma necessidade essencial no desenvolvimento da humanidade, assim que os primeiros homens dotados da capacidade de refletir os fenômenos a sua volta utilizaram-se dos conhecimentos para promover uma vida melhor. A Física Clássica tem seu momento de esplendor na Grécia Antiga, tendo como nome principal Aristóteles. Entrou em declínio na Idade Média, tendo revivido apenas durante o Renascimento, durante a Revolução Científica. | + | A ciência da física mecânica surge com uma necessidade essencial no desenvolvimento da humanidade, assim que os primeiros homens dotados da capacidade de refletir os fenômenos a sua volta utilizaram-se dos conhecimentos para promover uma vida melhor. A Física Clássica tem seu momento de esplendor na Grécia Antiga, tendo como nome principal Aristóteles. Entrou em declínio na Idade Média, tendo revivido apenas durante o Renascimento, durante a [https://pt.wikipedia.org/wiki/Revolu%C3%A7%C3%A3o_cient%C3%ADfica Revolução Científica]. |
Já dotado de um método científico devido aos vários pensadores como Galileu e Kepler, a Física teve uma notável evolução com Isaac Newton, que realizou a primeira grande unificação da Física ao unir Céus e Terra sob as mesmas leis da Física, a gravitação universal. | Já dotado de um método científico devido aos vários pensadores como Galileu e Kepler, a Física teve uma notável evolução com Isaac Newton, que realizou a primeira grande unificação da Física ao unir Céus e Terra sob as mesmas leis da Física, a gravitação universal. | ||
Ainda que a teoria feita fosse extremamente sólida e consistente, outros modelos surgem afim de abrir o leque de possibilidades na resolução de problemas antes complexos demais. Destaque-se os modelos Lagrangiano e Hamiltoniano, que investem numa alternativa de pensar usando energia fundamentalmente. | Ainda que a teoria feita fosse extremamente sólida e consistente, outros modelos surgem afim de abrir o leque de possibilidades na resolução de problemas antes complexos demais. Destaque-se os modelos Lagrangiano e Hamiltoniano, que investem numa alternativa de pensar usando energia fundamentalmente. | ||
| Linha 12: | Linha 12: | ||
=== Newton === | === Newton === | ||
| − | Isaac Newton<ref> | + | Isaac Newton<ref>http://pt.wikipedia.org/wiki/Isaac_Newton</ref> (4 de Janeiro de 1643 — Londres, 31 de março de 1727) foi um cientista inglês, mais reconhecido como físico e matemático, embora tenha sido também astrônomo, alquimista, filósofo natural e teólogo. |
Sua obra, Philosophiae Naturalis Principia Mathematica, é considerada uma das mais influentes na história da ciência. Publicada em 1687, esta obra descreve a lei da gravitação universal e as três leis de Newton, que fundamentaram a mecânica clássica. | Sua obra, Philosophiae Naturalis Principia Mathematica, é considerada uma das mais influentes na história da ciência. Publicada em 1687, esta obra descreve a lei da gravitação universal e as três leis de Newton, que fundamentaram a mecânica clássica. | ||
| Linha 21: | Linha 21: | ||
A construção da mecânica newtoniana está fundamentada nas três seguintes leis: | A construção da mecânica newtoniana está fundamentada nas três seguintes leis: | ||
| − | * 1ª Lei | + | * '''1ª Lei''' |
"Um corpo em repouso tende a permanecer em repouso, e um corpo em movimento tende a permanecer em movimento." | "Um corpo em repouso tende a permanecer em repouso, e um corpo em movimento tende a permanecer em movimento." | ||
Então, conclui-se que um corpo só altera seu estado de inércia, se alguém, ou alguma coisa aplicar nele uma força resultante diferente se zero. | Então, conclui-se que um corpo só altera seu estado de inércia, se alguém, ou alguma coisa aplicar nele uma força resultante diferente se zero. | ||
| − | * 2ª Lei | + | * '''2ª Lei''' |
A segunda lei de Newton diz que a Força é sempre diretamente proporcional ao produto da aceleração de um corpo pela sua massa, ou seja: | A segunda lei de Newton diz que a Força é sempre diretamente proporcional ao produto da aceleração de um corpo pela sua massa, ou seja: | ||
| Linha 43: | Linha 43: | ||
A unidade de força, no sistema internacional, é o N (Newton), que equivale a kg m/s² (quilograma metro por segundo ao quadrado). | A unidade de força, no sistema internacional, é o N (Newton), que equivale a kg m/s² (quilograma metro por segundo ao quadrado). | ||
| − | * 3ª Lei | + | * '''3ª Lei''' |
Esta é o princípio da ação e reação, cujo enunciado é: | Esta é o princípio da ação e reação, cujo enunciado é: | ||
| Linha 53: | Linha 53: | ||
=== Lagrange === | === Lagrange === | ||
| − | Joseph Louis Lagrange<ref> | + | Joseph Louis Lagrange<ref>http://pt.wikipedia.org/wiki/Joseph-Louis_Lagrange</ref> (Turim, 25 de janeiro de 1736 — Paris, 10 de abril de 1813) foi um matemático italiano. O pai de Lagrange havia sido tesoureiro de guerra da Sardenha, tendo se casado com Marie-Thérèse Gros, filha de um rico físico. Foi o único de dez irmãos que sobreviveu à infância. Napoleão Bonaparte fez dele senador, conde do império e grande oficial da Legião de Honra. |
A mecânica de Lagrange ou mecânica lagrangiana, nomeada em honra ao seu conceptor, Joseph-Louis Lagrange, é uma formulação da mecânica clássica que combina a conservação do momento linear com a conservação da energia. Exposta pela primeira vez no livro Méchanique Analytique em 1788, a formulação é provida de um potente ferramental matemático equivalente a qualquer outra formulação da mecânica, como por exemplo, o formalismo newtoniano. | A mecânica de Lagrange ou mecânica lagrangiana, nomeada em honra ao seu conceptor, Joseph-Louis Lagrange, é uma formulação da mecânica clássica que combina a conservação do momento linear com a conservação da energia. Exposta pela primeira vez no livro Méchanique Analytique em 1788, a formulação é provida de um potente ferramental matemático equivalente a qualquer outra formulação da mecânica, como por exemplo, o formalismo newtoniano. | ||
| Linha 61: | Linha 61: | ||
[[Arquivo:hamilton.jpg|200px|thumb|right|Hamilton]] | [[Arquivo:hamilton.jpg|200px|thumb|right|Hamilton]] | ||
| − | O personagem principal dessa sessão é | + | O personagem principal dessa sessão é [http://www-history.mcs.st-and.ac.uk/Biographies/Hamilton.html William Rowan Hamilton] (Dublin, 4 de agosto de 1805 — Dublin, 2 de setembro de 1865). Hamilton foi um físico, matemático e astrônomo irlandês |
Mecânica hamiltoniana é uma reformulação da mecânica clássica que foi elaborada em 1833 pelo matemático irlandês William Rowan Hamilton. Originou-se da mecânica lagrangiana, outra reformulação da mecânica clássica, introduzida por Joseph Louis Lagrange em 1788. Ela pode entretanto ser formulada sem recorrer a mecânica lagrangiana, usando espaços simpléticos. Veja a seção sobre esta formulação matemática para isto. O método hamiltoniano difere do lagrangiano em que ao invés de expressar confinamentos diferenciais de segunda ordem sobre um espaço coordenado n-dimensional, ela expressa confinamentos de primeira ordem sobre um espaço de fases 2n-dimensional. | Mecânica hamiltoniana é uma reformulação da mecânica clássica que foi elaborada em 1833 pelo matemático irlandês William Rowan Hamilton. Originou-se da mecânica lagrangiana, outra reformulação da mecânica clássica, introduzida por Joseph Louis Lagrange em 1788. Ela pode entretanto ser formulada sem recorrer a mecânica lagrangiana, usando espaços simpléticos. Veja a seção sobre esta formulação matemática para isto. O método hamiltoniano difere do lagrangiano em que ao invés de expressar confinamentos diferenciais de segunda ordem sobre um espaço coordenado n-dimensional, ela expressa confinamentos de primeira ordem sobre um espaço de fases 2n-dimensional. | ||
Como com a mecânica lagrangiana, as equações de Hamilton fornecem uma maneira nova e equivalente de olhar mecanismos clássicos. Geralmente, estas equações não fornecem uma maneira mais conveniente de resolver um problema particular. Entretanto, fornecem introspecções mais profundas na estrutura geral de mecanismos clássicos e em sua conexão aos mecânicos quânticos como compreendidos através dos mecânicos hamiltonianos, assim como suas conexões a outras áreas da ciência. | Como com a mecânica lagrangiana, as equações de Hamilton fornecem uma maneira nova e equivalente de olhar mecanismos clássicos. Geralmente, estas equações não fornecem uma maneira mais conveniente de resolver um problema particular. Entretanto, fornecem introspecções mais profundas na estrutura geral de mecanismos clássicos e em sua conexão aos mecânicos quânticos como compreendidos através dos mecânicos hamiltonianos, assim como suas conexões a outras áreas da ciência. | ||
Outros trabalhos importantes foram em torno do desenvolvimento da óptica e álgebra. A sua descoberta mais importante em matemática é a dos quaterniões, embora seu trabalho mais conhecido tenha sido na mecânica. | Outros trabalhos importantes foram em torno do desenvolvimento da óptica e álgebra. A sua descoberta mais importante em matemática é a dos quaterniões, embora seu trabalho mais conhecido tenha sido na mecânica. | ||
| − | |||
| − | |||
| − | |||
= Mecânica relativística = | = Mecânica relativística = | ||
| Linha 83: | Linha 80: | ||
: <math> E = m.c^2</math> | : <math> E = m.c^2</math> | ||
= Bibliografia = | = Bibliografia = | ||
| − | [http://www.wikipedia.org Wikipedia] | + | * [http://www.wikipedia.org Wikipedia] |
| − | http://pt.wikipedia.org/wiki/Hist%C3%B3ria_da_f%C3%ADsica | + | * http://pt.wikipedia.org/wiki/Hist%C3%B3ria_da_f%C3%ADsica |
| − | http:// | + | * http://www.sofisica.com.br/conteudos/Mecanica/Dinamica/leisdenewton.php |
| − | http://pt.wikipedia.org/wiki/ | + | * http://pt.wikipedia.org/wiki/Mec%C3%A2nica_de_Lagrange |
| − | http://pt.wikipedia.org/wiki/Mec%C3% | + | * http://pt.wikipedia.org/wiki/William_Rowan_Hamilton |
| + | |||
| + | * http://pt.wikipedia.org/wiki/Mec%C3%A2nica_hamiltoniana | ||
| − | |||
<references/> | <references/> | ||
| + | |||
| + | = Referências = | ||
Edição atual tal como às 17h22min de 30 de outubro de 2014
Conteúdo[ocultar] |
[editar] Mecânica Clássica
[editar] Introdução
A ciência da física mecânica surge com uma necessidade essencial no desenvolvimento da humanidade, assim que os primeiros homens dotados da capacidade de refletir os fenômenos a sua volta utilizaram-se dos conhecimentos para promover uma vida melhor. A Física Clássica tem seu momento de esplendor na Grécia Antiga, tendo como nome principal Aristóteles. Entrou em declínio na Idade Média, tendo revivido apenas durante o Renascimento, durante a Revolução Científica. Já dotado de um método científico devido aos vários pensadores como Galileu e Kepler, a Física teve uma notável evolução com Isaac Newton, que realizou a primeira grande unificação da Física ao unir Céus e Terra sob as mesmas leis da Física, a gravitação universal. Ainda que a teoria feita fosse extremamente sólida e consistente, outros modelos surgem afim de abrir o leque de possibilidades na resolução de problemas antes complexos demais. Destaque-se os modelos Lagrangiano e Hamiltoniano, que investem numa alternativa de pensar usando energia fundamentalmente.
[editar] Newton
Isaac Newton[1] (4 de Janeiro de 1643 — Londres, 31 de março de 1727) foi um cientista inglês, mais reconhecido como físico e matemático, embora tenha sido também astrônomo, alquimista, filósofo natural e teólogo.
Sua obra, Philosophiae Naturalis Principia Mathematica, é considerada uma das mais influentes na história da ciência. Publicada em 1687, esta obra descreve a lei da gravitação universal e as três leis de Newton, que fundamentaram a mecânica clássica.
[editar] Leis de Newton
A construção da mecânica newtoniana está fundamentada nas três seguintes leis:
- 1ª Lei
"Um corpo em repouso tende a permanecer em repouso, e um corpo em movimento tende a permanecer em movimento."
Então, conclui-se que um corpo só altera seu estado de inércia, se alguém, ou alguma coisa aplicar nele uma força resultante diferente se zero.
- 2ª Lei
A segunda lei de Newton diz que a Força é sempre diretamente proporcional ao produto da aceleração de um corpo pela sua massa, ou seja:
ou em módulo: F = ma
Onde:
F é a resultante de todas as forças que agem sobre o corpo (em N);
m é a massa do corpo a qual as forças atuam (em kg);
a é a aceleração adquirida (em m/s²).
A unidade de força, no sistema internacional, é o N (Newton), que equivale a kg m/s² (quilograma metro por segundo ao quadrado).
- 3ª Lei
Esta é o princípio da ação e reação, cujo enunciado é:
"As forças atuam sempre em pares, para toda força de ação, existe uma força de reação."
Quando uma pessoa empurra um caixa com um força F, podemos dizer que esta é uma força de ação. mas conforme a 3ª lei de Newton, sempre que isso ocorre, há uma outra força com módulo e direção iguais, e sentido oposto a força de ação, esta é chamada força de reação. Fim da conversa no bate-papo
[editar] Lagrange
Joseph Louis Lagrange[2] (Turim, 25 de janeiro de 1736 — Paris, 10 de abril de 1813) foi um matemático italiano. O pai de Lagrange havia sido tesoureiro de guerra da Sardenha, tendo se casado com Marie-Thérèse Gros, filha de um rico físico. Foi o único de dez irmãos que sobreviveu à infância. Napoleão Bonaparte fez dele senador, conde do império e grande oficial da Legião de Honra.
A mecânica de Lagrange ou mecânica lagrangiana, nomeada em honra ao seu conceptor, Joseph-Louis Lagrange, é uma formulação da mecânica clássica que combina a conservação do momento linear com a conservação da energia. Exposta pela primeira vez no livro Méchanique Analytique em 1788, a formulação é provida de um potente ferramental matemático equivalente a qualquer outra formulação da mecânica, como por exemplo, o formalismo newtoniano.
[editar] Hamilton
O personagem principal dessa sessão é William Rowan Hamilton (Dublin, 4 de agosto de 1805 — Dublin, 2 de setembro de 1865). Hamilton foi um físico, matemático e astrônomo irlandês Mecânica hamiltoniana é uma reformulação da mecânica clássica que foi elaborada em 1833 pelo matemático irlandês William Rowan Hamilton. Originou-se da mecânica lagrangiana, outra reformulação da mecânica clássica, introduzida por Joseph Louis Lagrange em 1788. Ela pode entretanto ser formulada sem recorrer a mecânica lagrangiana, usando espaços simpléticos. Veja a seção sobre esta formulação matemática para isto. O método hamiltoniano difere do lagrangiano em que ao invés de expressar confinamentos diferenciais de segunda ordem sobre um espaço coordenado n-dimensional, ela expressa confinamentos de primeira ordem sobre um espaço de fases 2n-dimensional. Como com a mecânica lagrangiana, as equações de Hamilton fornecem uma maneira nova e equivalente de olhar mecanismos clássicos. Geralmente, estas equações não fornecem uma maneira mais conveniente de resolver um problema particular. Entretanto, fornecem introspecções mais profundas na estrutura geral de mecanismos clássicos e em sua conexão aos mecânicos quânticos como compreendidos através dos mecânicos hamiltonianos, assim como suas conexões a outras áreas da ciência. Outros trabalhos importantes foram em torno do desenvolvimento da óptica e álgebra. A sua descoberta mais importante em matemática é a dos quaterniões, embora seu trabalho mais conhecido tenha sido na mecânica.
[editar] Mecânica relativística
[editar] Introdução
Ao longo dos anos, enquanto a teoria da mecânica clássica acumulava sucessos, chegou-se a pensar que ela descreveria com precisão absoluta o movimento de todos os corpos. Isso mudou, no entanto, a partir do início deste século XX. Com a evolução das técnicas de observação do universo físico foi possível conhecer novos fenômenos. Ao lado disso, a procura de uma consistência nas bases das duas teorias físicas até então bem estabelecidas, a mecânica clássica que descreve os movimentos e a eletrodinâmica clássica que trata dos fenômenos associados às cargas, levou à necessidade de se investigar algumas ideias bem aceitas na Física. Estes dois tipos de movimento na Física, o avanço experimental e a busca de uma consistência teórica, acabaram por levar a uma revolução no entendimento do universo físico. Na mecânica, esta revolução ocorreu através da teoria da relatividade e da física quântica.
A primeira grande mudança veio nos trabalhos de Einstein (1879 - 1955) na chamada Teoria da Relatividade saiba mais. Ela foi motivada na já citada inconsistência teórica nas bases da mecânica clássica e na eletrodinâmica, e utilizou conhecimentos de Lorentz sobre a necessidade de novas regras de transformação do espaço e do tempo. Lorentz havia descoberto que tipo de transformação deveria haver entre o espaço e o tempo de dois referenciais com velocidade relativa constante, que tornava a eletrodinâmica uma teoria válida para quaisquer referenciais inerciais. Essas transformações ficaram conhecidas como transformações de Lorentz, que são diferentes das transformações de Galileu, válidas na mecânica clássica.
- Albert Einstein *[1]
- Hendrik Lorentz Página destinada da Wikipédia