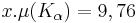Mudanças entre as edições de "Teced/textos/Grupo50"
| Linha 1: | Linha 1: | ||
| − | |||
Edição atual tal como às 21h18min de 12 de setembro de 2011
[editar] Resumo
Realizamos uma investigação acerca das radiações de raios X, utilizando um difratômetro automatizado que nos fornecia espectros de intensidade por ângulo de detecção do espalhamento dessas radiações. Neste equipamento, um feixe de elétrons era acelerado em direção a um alvo de Molibdênio (Mo) e durante o processo ocorria emissão de espectro de radiação com energias da ordem de keV. Verificamos que para uma energia menor que a energia de ionização do alvo de Mo, o espectro apresentava-se contínuo, porém para energias maiores que esta, o espectro apresentava picos, o que nos levou a concluir que o espectro era formado pela superposição de dois tipos de radiação: uma devido à desaceleração dos elétrons ao se aproximarem do alvo de Mo e outra devido à interação destes elétrons com os átomos de Mo (ionização), aqui chamadas de K α e K β . Também conseguimos, através de um filtro de Zircônio, polarizar esta radiação fazendo com que só o atravessasse a radiação K α . Esta polarização só foi possível pelo fato da energia de ionização de nosso polarizador (Zr) possuir um valor entre as energias de K α e K β . Finalmente, utilizando a radiação polarizada, estudamos a difração num alvo de monocristal de NaCl, desvendando sua geometria molecular.
[editar] Introdução - Raios X
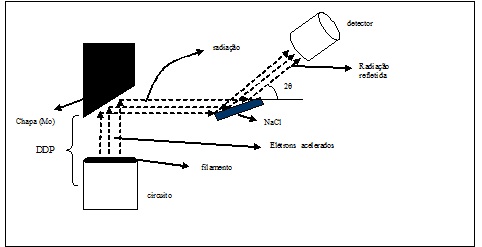
Os raios X são radiações eletromagnéticas com comprimento de onda menor que aproximadamente 1,0 Å e apresentam propriedades típicas de ondas como polarização, interferência e difração, da mesma forma que todas as outras radiações eletromagnéticas, sendo que algumas destas propriedades serão verificadas neste experimento. Eles são produzidosno alvo de um tubo de raios X, quando um feixe de elétrons de alta energia, acelerados por uma diferença de potencial de alguns milhares de volts, é freado ao atingir o alvo, como mostrado na figura abaixo onde os raios x são representados pelos vetores em vermelho. Segundo a física clássica, a desaceleração dos elétrons, freados pelo material do alvo, causa a emissão de um espectro contínuo de radiação eletromagnética.
Para interpretar os processos aqui estudados, é necessário supor que cada elétron envolvido espalha um quantum completo de radiação (fóton), que interage com a matéria. O elétron interage com o núcleo carregado através do campo coulombiano, transferindo momento para o núcleo. A desaceleração resultante causa a emissão do fóton. Também é necessário o uso da teoria ondulatória da radiação para interpretar os fenômenos de interferência e difração e polarização. Daí a importância deste experimento: devemos supor um caráter dual da radiação eletromagnético, que marcou definitivamente a transição da Física. Este experimento foi realizado em três etapas, que foram analisadas separadamente.
[editar] Etapa 1 - Análise do espectro de emissão de um tubo de Raios X
Nesta etapa, fizemos incidir elétrons "arrancados" de um circuito por uma ddp aplicada contra uma chapa de Molibdênio. Ao alcançarem a chapa de molibdênio, os elétrons emitiram radiação que era direcionada para um alvo de cristal de cloreto de sódio (NaCl), onde ocorria difração e emissão de um espectro que foi analisado sob diversos parâmetros: a ddp utilizada para arrancar os elétrons do circuito, a corrente no circuito e o ângulo de espalhamento.
Verificamos que o espectro emitido poderia ser explicado como uma superposição de um espectro contínuo que depende apenas da energia dos elétrons do feixe e é oriundo da desaceleração dos elétrons ao se aproximarem do alvo de Mo, e um espectro discreto que é característico do elemento utilizado como alvo, no presente caso, o Molibdênio. Este espectro discreto que apresentou dois picos bem definidos, aqui chamados de K α e K β , é emitido quando os elétrons do feixe transferem energia suficiente para ionizar elétrons da camada K do Mo, formando espaços vazios que logo são preenchidos por elétrons das camadas L e M. Os fótons emitidos pelos elétrons que executam este tipo de transição possuem energia na ordem de KeV, portanto, na freqüência de raio-x, que era detectada por nosso equipamento. Nesta etapa estimamos os valores de energia e comprimento de onda de K α e K β , através da aplicação da Lei de Bragg e discutimos os efeitos da ddp e da corrente nos espectros.
[editar] Descrição experimental
O equipamento utilizado foi um tubo de raio-x automatizado, modelo Roentingengerat- X-Ray Aparatus, formado por um circuito com filamento de tungstênio no qual se formava um nuvem eletrônica quando percorrido por uma corrente elétrica i, uma chapa de Molibdênio (Mo) carregada positivamente, um anteparo de cristal (NaCl) e um detector de raios X.
Para que os elétrons do filamento de tungstênio fossem arrancados em direção à chapa, foi imposta uma ddp entre o circuito e a chapa, conforme o esquema ilustrado pela figura \ref{fig:arranjo2}.
O equipamento realizava a contagem de fótons incidentes em seu detector para um determinado ângulo $ \theta $ de espalhamento do feixe de raios X pelo cristal de NaCl, por unidade de tempo. A interface deste equipamento possibilitava ajustes: nos ângulos de medição entre a direção do feixe incidente e o feixe espalhado; no intervalo de contagem para cada ângulo; na diferença de potencial (ddp) aplicada entre o circuito (filamento) e a chapa de tungstênio; e na corrente (i) do circuito.
O equipamento fornecia o número de contagens por segundo, relativa aos fótons que eram espalhados para cada ângulo. Vale ressaltar que o número fornecido pelo equipamento (contagen de fótons) era proporcional e não idêntico ao número de fótons que chegavam ao detector num intervalo de tempo de um segundo, para cada ângulo $ \theta $.
Realizamos a tomada de dados para 4 condições iniciais diferentes, todas controladas automaticamente por nosso equipamento, formando 4 espectros, conforme a tabela:
| Espectro | ddp (kV) | i (mA) | Tempo (s) | Intervalo (grau) |
| 1 | 35 | 1 | 5 | 2,5o < θ < 12,5o |
| 2 | 27 | 1 | 10 | 2,5o < θ < 12,5o |
| 3 | 20 | 1 | 20 | 2,5o < θ < 12,5o |
| 4 | 35 | 0,5 | 10 | 2,5o < θ < 12,5o |
Lista de condições iniciais para tomada dos espectros.
Vale ressaltar que o cristal de NaCl utilizado no equipamento tratava-se de um monocristal, ou seja, sua estrutura molecular era alinhada de modo a evitar o aparecimento de halos de difração que dificultassem a análise de seu espectro.
[editar] Resultados
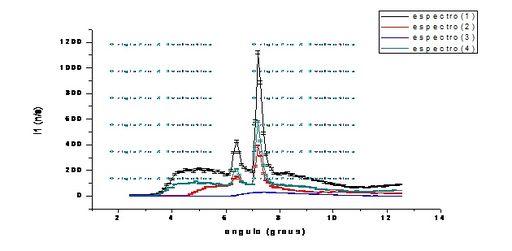
O equipamento nos forneceu os resultados constantes na tabela A, em anexo, ou seja, intensidade (contagem de fótons por segundo) para cada ângulo de difração, em cada uma das condições iniciais descritas na tabela \ref{tab:tabelaEspectros}, para as quais construímos o gráfico I x θ,e aplicando a relação de Bragg:
onde \textit{d} era a distância entre os planos atômicos do NaCl, cujo valor tabelado é $ d = 2,8 Å $, pudemos relacionar o ângulo de espalhamento com o comprimento de onda da radiação, construindo o gráfico I x λ e finalmente aplicando a relação de Einstein:
pudemos relacionar o comprimento de onda com a energia da radiação, tornando possível a construção do gráfico I x E.
A incerteza na intensidade foi obtida através da aplicação, ponto a ponto, da fórmula  onde I é a intensidade(contagem por segundo) medida pelo detector e t é o tempo que o aparelho mediu a intensidade em cada ângulo de espalhamento. Percebemos que quanto menor o tempo de medição, maior é a incerteza estatística, por isso o espectro 1 apresenta maior incerteza.
onde I é a intensidade(contagem por segundo) medida pelo detector e t é o tempo que o aparelho mediu a intensidade em cada ângulo de espalhamento. Percebemos que quanto menor o tempo de medição, maior é a incerteza estatística, por isso o espectro 1 apresenta maior incerteza.
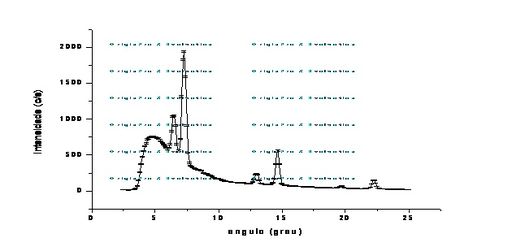
Analisando os gráficos, supomos a sobreposição de 2 tipos de curva: uma curva contínua devido a emissão de fótons pela desaceleração dos elétrons emitidos pelo filamento de tungstênio ao se aproximarem da chapa de Molibdênio (radiação de Bremsstrahlung) e outra curva discreta (com picos) devido a interação destes elétrons com os átomos de Mo, ocasionando, dependendo da energia destes elétrons, a emissão de radiações aqui denominadas K α e K β . Estes picos, conforme os gráficos demonstram, ocorreram para os valores da tabela \ref{tab:tabelaPicos}.
| Radiação | Ângulo (rad) | Energia (keV) | λ (Å) |
| K α | 5,51(7)x10-2 | 17,6(2) | 0,71(3) |
| K β | 6,25(7)x10-2 | 19,8(2) | 0,62(3) |
Valores dos picos K α e K β com base nos gráficos das figuras TodosEspectrosXlambda e TodosEspectrosXenergia.
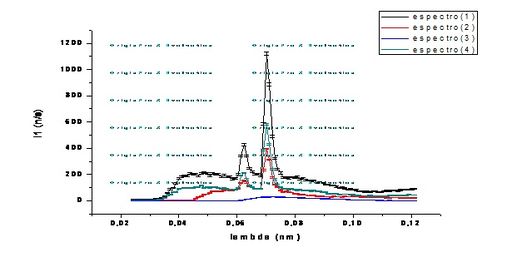
Vale ressaltar que a parte dessa radiação que foi emitida pela interação com a chapa de Molibdênio pode ser explicada como fruto da transição de elétrons da camada L para a camada K e da camada M para a camada K dos átomos de Mo, obedecendo a regra de transição eletrônica de Pauli. Quando os elétrons incidentes na chapa de Mo forneciam energia suficiente para os elétrons da camada K destes átomos vencerem o potencial que os mantinham presos à eletrosfera, elétrons de camadas superiores (L e M) realizavam a transição para ocupar os elétrons retirados da camada K. Como há diferença energética entre estas camadas, ao efetuar a transição os elétrons emitem um quantum de energia (fóton) com comprimento de onda na ordem de grandeza da radiação chamada de raios X, conforme o esquema ilustrativo da figura Diagrama_energetico.
A radiação emitida pela chapa de Mo (raio X) era então composta por radiação do tipo K α e do tipo K β , cada uma carregando uma quantidade definida de energia dada pela diferença entre as energias das camadas L e K e M e K, respectivamente.
Outro fato observado nestes espectros é a existência de um valor mínimo de comprimento de onda que dependia da ddp entre a chapa de Mo e o circuito, ou seja, da energia dos elétrons incidentes na placa de Mo.
Comparando os espectros obtidos para a mesma ddp (espectro 1 e 4, com 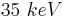 ), notamos que ambos apresentam o mesmo valor para o mínimo comprimento de onda, e este valor era diferente dos outros espectros, com ddp diferentes (
), notamos que ambos apresentam o mesmo valor para o mínimo comprimento de onda, e este valor era diferente dos outros espectros, com ddp diferentes (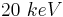 e
e  ).
).
A teoria eletromagnética clássica não pode explicar esse fato, pois não haveria razão para que ondas com comprimento de onda menor do que os observados não fossem emitidos pelo alvo, pois ali não há uma relação explícita entre energia e comprimento de onda (ou seja, entre partícula e onda). Porém, ao encararmos os raios-x como fótons o processo torna-se elementar.
Um elétron com energia cinética K (dada pela ddp a que foi submetido) é desacelerado pela interação com o núcleo pesado dos átomos de Mo e a energia que ele perde aparece na forma de fótons de raios X. A massa do núcleo de Mo é tão grande comparada à massa do elétron, que a energia que ele adquire após a interação pode ser desprezada. Então, sendo K' a energia cinética do elétron após a colisão, a energia do fóton emitido será:
O fóton com menor energia, ou maior comprimento de onda, seria emitido quando o elétron incidente perdesse toda sua energia cinética, ou seja, K'=0, de forma que
Em nosso caso (espectros 1 e 4), K = 35 KeV, logo:
O valor de  para os espectros 1 e 4 (com mesma ddp) obtido analisando o gráfico da figura TodosEspectrosXlambda foi
para os espectros 1 e 4 (com mesma ddp) obtido analisando o gráfico da figura TodosEspectrosXlambda foi 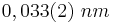 , sendo, portanto, compatível com o resultado previsto pelos cálculos acima apresentados.
, sendo, portanto, compatível com o resultado previsto pelos cálculos acima apresentados.
Efetuando a comparação entre espectros obtidos com a mesma corrente no circuito e diferentes ddp (espectros 1 e 2)percebemos que o espectro 1( e
e 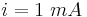 ) possui
) possui  menor do que o espectro 2(
menor do que o espectro 2(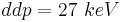 e
e 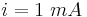 ) e intensidade do espectro 1 é maior do que a intensidade de emissão do espectro 2. Isso ocorre porque com maior ddp, mais elétrons são extraídos do circuito em direção ao cátodo de Mo, portanto há maior emissão de raios X e consequentemente maior contagem de nosso equipamento; a energia cinética (K) desses elétrons também é maior devido a maior ddp, por isso
) e intensidade do espectro 1 é maior do que a intensidade de emissão do espectro 2. Isso ocorre porque com maior ddp, mais elétrons são extraídos do circuito em direção ao cátodo de Mo, portanto há maior emissão de raios X e consequentemente maior contagem de nosso equipamento; a energia cinética (K) desses elétrons também é maior devido a maior ddp, por isso  é menor (maior energia máxima).
é menor (maior energia máxima).
Como corrente elétrica é a quantidade de elétrons que atravessa uma secção transversal do condutor num intervalo de tempo, concluímos que quando aumentamos a corrente, mais elétrons são extraídos do circuito por unidade de tempo, portanto, maior emissão de fótons de raios X, aumentando a intensidade do espectro.
Porém, antes de serem detectados por nosso equipamento, estes fótons incidiam num cristal de NaCl, sofrendo espalhamento com picos bem definidos para dois valores de $\theta$. A existência destes dois picos demonstram qualitativamente a validade dos postulados de De Broglie, pois eles só podem ser explicados como uma interferência construtiva de ondas espalhadas pelo arranjo periódico dos átomos nos planos do cristal de NaCl. Portanto, esses fótons que assumiram o caráter de partículas portadoras de um quantum de energia para explicar a existência de um  nos espectros 1 e 4 sujeitos a uma mesma ddp, agora devem assumir um caráter ondulatório para explicar seu espalhamento pelo cristal conforme ilustração da figura LeiBragg.
nos espectros 1 e 4 sujeitos a uma mesma ddp, agora devem assumir um caráter ondulatório para explicar seu espalhamento pelo cristal conforme ilustração da figura LeiBragg.
Os picos de K α e K β observados no gráfico TodosEspectrosXangulo devem ser fruto de consecutivas interferências construtivas entre K α e K β nos vários planos do cristal, para diversos ângulos de incidência no NaCl. Talvez se conseguíssemos "filtrar" apenas um destes tipos de radiação, obteríamos picos mais definidos em certos valores de ângulo de difração, sendo possível uma análise mais aprofundada sobre a geometria molecular do NaCl. Esta análise foi realizada na 3ªparte deste experimento.
Como o espectro 3 não apresenta picos, supomos que os elétrons emitidos naquela ddp ( ) não forneciam energia suficiente aos elétrons dos átomos de Mo para arrancá-los da camada K, não havendo, portanto, emissão de K α e K β , portanto o aspecto contínuo de sua curva seria apenas devido as emissões oriundas do freamento dos elétrons ao se aproximarem da chapa de Mo, pois, ao desacelerarem, esses elétrons devem emitir radiação num espectro sem picos(contínuo), enquadrando-se em nossa hipótese de sobreposição de curvas. Podemos intuir também que a energia necessária para retirar elétrons da camada K dos átomos de Mo se encontra num intervalo entre
) não forneciam energia suficiente aos elétrons dos átomos de Mo para arrancá-los da camada K, não havendo, portanto, emissão de K α e K β , portanto o aspecto contínuo de sua curva seria apenas devido as emissões oriundas do freamento dos elétrons ao se aproximarem da chapa de Mo, pois, ao desacelerarem, esses elétrons devem emitir radiação num espectro sem picos(contínuo), enquadrando-se em nossa hipótese de sobreposição de curvas. Podemos intuir também que a energia necessária para retirar elétrons da camada K dos átomos de Mo se encontra num intervalo entre 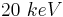 (sem picos) e
(sem picos) e 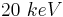 (já com picos relativos à K α e K β ).
(já com picos relativos à K α e K β ).
[editar] Etapa 2 - Análise do espectro de absorção por filtro de Zircônio (Zr)
Nesta etapa fizemos a radiação proveniente da chapa de molibdêdio incidir numa placa de Zircônio com o intuito de explorar o fenômeno de absorção de raios X. Através da análise dos espectros de absorção pudemos concluir que o Zr é um bom filtro para a radiação proveniente do Mo, já que ele permite a passagem de apenas um comprimento de onda, polarizando a radiação e eliminando as possíveis interações entre K α e K β nos diversos ângulos de difração no cristal, fato já mencionado na parte 1 deste relatório. Conhecendo o espectro de absorção do Zr, pudemos estimar sua energia de ionização.
[editar] Descrição experimental
Utilizamos o mesmo difratômetro mencionado na seção Etapa 1, porém, desta vez, utilizamos um filtro de Zircônio sobre o qual a radiação proveniente da chapa de Mo incidia. Realizamos medições do número de contagens por segundo de fótons incidentes para cada ângulo varrido por nosso equipamento primeiramente sem o filtro de Zr (I 0 ), e posteriormente com o filtro de Zr (I), nas condições apresentadas na tabela:
| Espectro | ddp (kV) | i (mA) | Tempo (s) | Intervalo (grau) |
| Sem filtro | 35 | 1 | 10 | 2,5o < θ < 30o |
| Com filtro | 35 | 1 | 10 | 2,5o < θ < 30o |
Lista de condições iniciais para tomada dos espectros com o filtro de zircônio.
[editar] Resultados
Através dos dados obtidos elaboramos a tabela B, em anexo, e plotamos o gráfico da figura Comparacao_com_sem_filtro comparando a intensidade do espectro detectado por nosso equipamento com e sem o filtro de Zr e também o gráfico da figura EspectroAbsorcao_Zr do espectro de absorção do Zr ( ) em função da energia da radiação, que foi obtida a partir da aplicação das equações de Bragg e de Einstein sobre os valores dos ângulos de medição.
) em função da energia da radiação, que foi obtida a partir da aplicação das equações de Bragg e de Einstein sobre os valores dos ângulos de medição.
Percebemos que, com o filtro, houve uma diminuição na intensidade do espectro (contagem de fótons por segundo), como era de se esperar, pois o filtro deveria absorver parte da radiação incidente através da lei de Lambert-Beer:
\label{eq:B1}
Onde 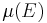 é o coeficiente de absorção do filtro (Zr) para um determinado comprimento de onda e x é a espessura do filtro. Porém fica evidente que a absorção foi muito maior a partir de "um certo" valor de energia, ligeiramente superior ao primeiro pico correspondente a K α . Este "corte" na intensidade do espectro foi observado numa energia em torno de
é o coeficiente de absorção do filtro (Zr) para um determinado comprimento de onda e x é a espessura do filtro. Porém fica evidente que a absorção foi muito maior a partir de "um certo" valor de energia, ligeiramente superior ao primeiro pico correspondente a K α . Este "corte" na intensidade do espectro foi observado numa energia em torno de 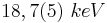 .
.
Uma explicação para este fenômeno é que a energia de ionização do Zr, ou seja, a energia necessária para retirar um elétron da camada K deste átomo, deve estar num valor entre K α e K β do Mo, fazendo com que a radiação K α fosse quase que inteiramente transmitida pelo filtro enquanto que K β , por possuir energia suficiente para ionizar o Zr, foi quase que totalmente absorvida por ele. Como o Zr, após esta absorção, emitiu seus próprios K α e K β com comprimentos de ondas específicos, diferentes da radiação emitida pelo Mo e não detectáveis por nosso equipamento, percebemos a grande diferença na intensidade dos espectros após este valor. Portanto podemos estimar que a energia de ionização dos átomos de Zr corresponde à energia onde ocorreu o "corte" no gráfico da figura Comparacao_com_sem_filtro, ou seja, algo em torno de 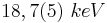 . Desta forma então conseguimos um método para "filtrar" K α , que será utilizado para anular suas interferências construtivas com K β ao fazê-lo incidir no cristal de NaCl, como veremos adiante.
. Desta forma então conseguimos um método para "filtrar" K α , que será utilizado para anular suas interferências construtivas com K β ao fazê-lo incidir no cristal de NaCl, como veremos adiante.
A incerteza de 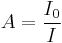 foi calculada através da fórmula de propagação de incertezas, aplicada ponto a ponto:
foi calculada através da fórmula de propagação de incertezas, aplicada ponto a ponto:
O gráfico da figura EspectroAbsorcao_Zr nos fornece o espectro de absorção do filtro de Zr em função da energia das radiações (obtidas a partir dos ângulos de detecção). Nesse gráfico, o pico maior representa a região de energia para a qual a absorção foi máxima, ou seja, a energia de ionização do Zr, cujo valor da meia altura pode ser observado em torno de 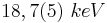 , em concordância com a região de corte do gráfico Comparacao_com_sem_filtro.
Apresentamos na tabela a seguir os valores obtidos para a energia de ionização do Zr, bem como para as energias de K α e K β , por todos os grupos que realizaram o experimento onde nossos dados aparecem na coluna referente ao grupo 2.
, em concordância com a região de corte do gráfico Comparacao_com_sem_filtro.
Apresentamos na tabela a seguir os valores obtidos para a energia de ionização do Zr, bem como para as energias de K α e K β , por todos os grupos que realizaram o experimento onde nossos dados aparecem na coluna referente ao grupo 2.
| Espectro (keV) | Grupo 1 | Grupo 2 | Grupo 3 | Grupo 4 | Valor tabelado |
| Ionização (Zr) | 18,71 | 18,7(5) | 19,37 | 18,85 | 18,54 |
| $K α | 17,67 | 17,6(2) | 17,92 | 17,67 | 17,48 |
| $K β | 19,87 | 19,8(2) | 20,19 | 20,17 | 19,61 \\ |
Resultados de K α e K β dos demais grupos de trabalho.
Percebemos que nossos dados são compatíveis, dentro de suas incertezas, com os valores tabelados.
Calculamos também o erro percentual (E%) do valor obtido para a energia de ionização do Zr:
Este resultado mostra a proximidade entre nosso resultado experimental e o valor tabelado para esta grandeza.
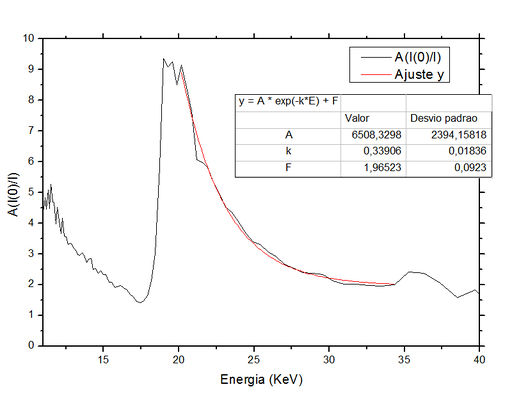
A fim de estimarmos o coeficiente de absorção do Zr para o comprimento de onda de K α , ajustamos a função à curva do gráfico da figura EspectroAbsorcao_Zr, empregando o software "Origin", obtendo o gráfico da figura AxE-ajuste_exp.
Escrevendo a equação na forma:
e fazendo  , pode-se escrever:
, pode-se escrever:
\label{eq:B2}
onde denominamos F a radiação de fundo observada no espectro.
e ainda, substituindo E pelo valor da energia de 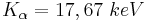 , obtivemos:
, obtivemos:
[editar] Etapa 3 - Análise do espectro de difração
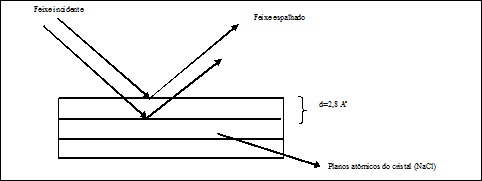
Após estabelecer um método de polarização da radiação emitida pela chapa de Mo através do filtro de Zr, passamos a investigar o espectro de difração da radiação polarizada ao incidir no cristal de NaCl. Sabemos que apenas a radiação K α atingiu o cristal, portanto, pudemos a partir do espectro obtido em função do ângulo de espalhamento,aplicar a relação de Bragg e inferir sobre a geometria molecular do NaCl, comparando com os valores conhecidos.
[editar] Descrição experimental
Utilizando o mesmo difratômetro fizemos incidir a radiação sobre um monocristal de NaCl. Nosso equipamento mediu a contagem de radiação por ângulo de espalhamento para duas situações, com filtro e sem filtro de zircônio, ambas com as condições de iniciais do equipamento apresentada na tabela abaixo:
| ddp (kV) | Corrente (mA) | Tempo (s) | Ângulo |
| 35 | 1 | 10 | 2,5o < 2\theta < 12,5o |
Condições iniciais do equipamento para a etapa 3 do experimento.
[editar] Resultados
Nosso equipamento nos forneceu os dados constantes na tabela C, em anexo, através da qual construímos os gráficos das figuras abaixo dos espectros emitidos, respectivamente, sem filtro e com filtro.
A incerteza na intensidade foi obtida através da aplicação, ponto a ponto, da fórmula:
Comparando os gráficos das figuras acima, verificamos que a utilização do filtro de Zr reduziu o número de picos de intensidade para o intervalo analisado. O significado deste fato é que os picos do gráfico sem filtro referem-se, além da interferência construtiva para os diversos ângulos θ , à presença de dois tipos de radiação (K α e K β ), portanto, seria difícil efetuar uma análise sobre a geometria do cristal aplicando a lei de Bragg neste espectro. Já o gráfico com filtro, mostra o espectro filtrado, ou seja, o espectro de K α , portanto seus picos certamente são decorrentes apenas da geometria do cristal, tornando possível sua análise.
Cada pico refere-se a uma ordem de difração ocorrida em um plano molecular do cristal, que aqui denotaremos com índice "n".
Através da análise dos picos do gráfico da figura "com filtro" e a aplicação da Lei de Bragg, construímos a tabela:
| n | Λ (K α ) | θ | 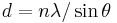
| |
| Pico 1 | 1 | 0,71(2) Å | $ 7,3(2)o $ | 2,79(2) |
| Pico 2 | 2 | 0,71(2) Å | $ 14,7(2)o $ | 2,80(2) |
| Pico 3 | 3 | 0,71(2) Å | $ 22,3(2)o $ | 2,81(2) |
Resultados obtidos aplicando-se a Lei de Bragg às medições realizadas.
Os valores encontrados para d são compatíveis com o valor tabelado (2,8 Å), o que demonstra a eficiência de nosso filtro de Zr para esta análise, validando a aplicação da Lei de Bragg.
[editar] Conclusões
Neste experimento verificamos que um feixe de elétrons ao ser acelerado contra um alvo de Molibdênio emite radiação na ordem de keV cujo espectro é formado por duas componentes que se superpõem: uma componente contínua, devido à desaceleração dos elétrons ao se aproximarem do alvo e que depende somente da energia desses elétrons (no caso, ddp) e outra discreta, devido à interação desses elétrons com os átomos que compões o alvo, onde ocorre a emissão de radiação com dois comprimentos de onda, aqui chamados de K α e K β , cujos valores pudemos determinar experimentalmente e comparar com os valores tabelados para essas radiações sendo, portanto, compatíveis dentro de suas incertezas.
| Radiação | Energia (keV) (exp.) | Energia (keV) (tabelado) |
| K α | 17,6(2) | 17,48 |
| K β | 19,8(2) | 19,61 |
Comparação dos resultados obtidos experimentalmente com os valores tabelados.
Concluímos também que o Zircônio é um bom filtro para as radiações provenientes do Molibdênio, pois sua energia de ionização encontra-se num valor intermediário entre as energias de K α e K β do molibdênio, sendo assim, a radiação K α , por possuir energia menor do que a necessária para ionizar elétrons da camada K do Zr, o atravessava obedecendo a lei de absorção de Lambert-Beer; já a radiação K β , por possuir energia suficiente para ionizar o Zr, era quase que totalmente absorvida por ele, para esse fim. Também pudemos, a partir da análise dos gráficos de absorção, calcular a energia de ionização do Zircônio: 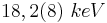 ,valor que se mostrou compatível com o valor tabelado.
,valor que se mostrou compatível com o valor tabelado.
Fazendo a radiação polarizada K α incidir numa lâmina de monocristal (NaCl), pudemos, após análise do espectro de difração, calcular a distância entre os planos atômicos do NaCl, d = 2,8(2) Å, compatível com o tabelado, sendo portanto válida a aplicação da Lei de Bragg.
[editar] Anexos
[editar] Anexo A
Tabela de dados referidas como Anexo A.
[editar] Anexo B
Tabela de dados referidas como Anexo B.
[editar] Anexo C
Tabela de dados referidas como Anexo C.
[editar] Biografia dos cientistas
[editar] Sir William Lawrence Bragg
OBE(Adelaide, 31 de Março de 1890 — Ipswich, 1 de Julho de 1971) foi um físico australiano. Recebeu em 1915, juntamente com seu pai William Henry Bragg, o Nobel de Física, por trabalhos na análise da estrutura cristalina através da difração de raios-X. É a pessoa mais jovem a ter sido contemplada com um prêmio Nobel: tinha, na época, apenas 25 anos de idade. Participou da 2ª, 3ª, 4ª e 5ª Conferência de Solvay, e foi presidente das conferências 8ª a 12ª.
[editar] Sir William Henry Bragg
KBE, OM, PhD, PRS (Wigton, Cumberland, 2 de Julho de 1862 — Londres, 10 de Março de 1942) foi um físico e químico britânico. Em 1915, recebeu com seu filho, William Lawrence Bragg, o Nobel de Física pelos trabalhos na análise da estrutura cristalina através da difração de raios-X
[editar] Wilhelm Conrad Röntgen
(Lennep, 27 de março de 1845 — Munique, 10 de fevereiro de 1923) foi um físico alemão que, em 8 de novembro de 1895, produziu radiação electromagnética nos comprimentos de onda correspondentes aos atualmente chamados raios-X.
[editar] Créditos pela elaboração desse relatório e da página Wiki
O presente relatório foi elaborado pelos alunos Eduardo Rodrigues da Silva, Evandro Bittencourt Cruz e Fábio Tesser Barzagli, todos estudantes de Licenciatura em Física no Instituto de Física da USP, por ocasião do curso Laboratório de Física Moderna, no 1º semestre de 2010.
Foi convertido para o formato página Wiki pelos alunos Eduardo Rodrigues da Silva, Carlos Honorato Deusdará e Thiago Augusto Cardoso, todos estudantes de Licenciatura em Física no Instituto de Física da USP, por ocasião do curso Tecnologia Educacional no Ensino de Física no 2º semestre de 2011.



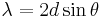
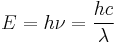


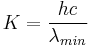
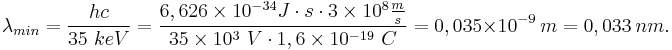


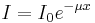

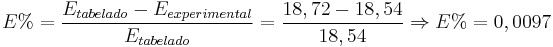
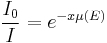
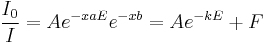
![x . \mu(E) = k . E + \ln(A) = [0,34.E + ln(6508,32)] = [0,34.E + 8,79]](/images/math/5/c/f/5cfba2018a351cb468c59b49058726bb.png)