Mudanças entre as edições de "Teced/textos/Grupo 5 13"

Edição das 22h19min de 11 de setembro de 2013

Conteúdo

1 Proposta
2 História
3 Modelos cineticos para o processo de termoluminescencia
4 Aplicações
5 Referências

Proposta

O grupo 5 - Bruno e Stevan propoe criar na wiki stoa e expandir o artigo da Wikipedia sobre Termoluminescência. Para compreender melhor o fenômeno de Termoluminescência (TL) , é necessário introduzir alguns conceitos básicos sobre a luminescência. Aluminescência é o fenômeno de emissão em forma de luz resultado de uma transição radiativa num átomo, íon, moçécula,radical ou cristal, de um estado eletrônico exitado ao estado fundamental ou a outro estado com menor energia. Ela pode ser considerada como uma conversão de outras formas de energia em luz.

Portanto ao termo Termoluminescência (TL) é a emissão luminescente proveniente de de um material, previamente irradiado, quando calor é adicionado artificialmente.

História

Segundo Becker (1973) há relatos de que alquimistas medievais já sabiam que certos minerais emitiam uma fraca luz no escuro quando os mesmos eram aquecidos.

Contudo, possivelmente o primeiro relato de caráter científico do fenômeno da termoluminescência foi feito em 1663 por Robet Boyle, que notou uma “luz esmaecida” de um diamante quando submetida a um processo de aquecimento.

Até 1940, ano em que foi inventada a fotomultiplicadora, o fenômeno da TL era utilizado, apenas, como ferramenta na identificação de minerais.

Estimulado pelos trabalhos de Farrington Daniels na universidade de Wisconsin, em 1950, o fenômeno da termoluminescência passou a ser utilizado para realizar medidas de exposição à radiação nuclear, além de outras aplicações.

Iniciou-se por volta deste período, também, o estudo do mecanismo envolvido com a termoluminescência, principalmente pelos trabalhos de Randall e

Wilkins, em 1945, que formularam um modelo teórico para a curva de emissão.

Todavia, a possibilidade do uso da termoluminescência na datação arqueológica e geológica só surgiu em 1953, sugerida por Daniels et al. (1953), e logo após com o trabalho apresentado por Kennedy e Knopf, em 1960, no Meeting of American Association for the Advance of Science,relatando resultados de datação por TL de amostras arqueológicas e de lava (Santos, 2002).

Neste mesmo ano Grögler et al. (Tatumi, 1987) detectou que amostras cerâmicas apresentavam o fenômeno da termoluminescência, levantando assim, o potencial de utilização destes materiais para datação arqueológica.

Em 1961, os trabalhos de datação de amostras geológicas por termoluminescência tomaram um grande impulso com os trabalhos de Johnson (Aitken; 1985), datando rochas presentes nas proximidades da intrusão da lava, a fim de determinar a época em que a mesma fluiu pela região.

Porém, nesta época, os pesquisadores encontravam diversas dificuldades na utilização da termoluminescência para datação arqueológica e geológica, pois a quantidade de impurezas presentes nas amostras já era um fato bastante conhecido, mas não havia sido feito um estudo do seu papel na TL.

Subseqüentemente, com o estudo do mecanismo e do papel das impurezas na TL, McDougall (1968) em (Santos, 2002), a termoluminescência passou a

ser utilizada para datação arqueológica em diversos laboratórios pelo mundo.

Imediatamente, após o início da década de 70, surgiram extensões do uso da datação por termoluminescência para diversos materiais, como argilas queimadas, que potencialmente apresentam-se como uma ferramenta para o estudo da paleontologia, onde o método do carbono 14 é limitado; a calcita para datação de estalagmite e a lava vulcânica para estudo em geologia, etc.

No Brasil, as primeiras datações por TL foram feitas no Instituto de Física da USP, por Szmuk e Watanabe em 1971, quando dataram vasos cerâmicos e urnas funerárias encontradas no interior de São Paulo, dando seqüência a diversos trabalhos em vários sítios arqueológicos pelo Brasil, como no Parque Nacional do Xingú Miyamoto e Watanabe.(1974), Araripe no Norte do Brasil Matsuoka (1984),(Santos,2002).

Atualmente, têm sido feitas diversas datações por TL de materiais provenientes de diversos locais do Brasil, realizadas pelo Laboratório de Vidros da FATEC/SP, no Instituto de Física da USP.

Em Sergipe, o potencial para datação arqueológica foi levantado após a implantação do Laboratório de Caracterização de Materiais, posteriormente, Laboratório de Preparação e Caracterização de Materiais (LPCM), em 1992, no Departamento de Física da Universidade

Federal de Sergipe (UFS) e com a implantação do Projeto Arqueológico de Xingó, pois nos sítios escavados na região foram encontradas grandes quantidades de materiais cerâmicos, levantando a possibilidade de formação de um grupo de datação arqueológica por TL no

LPCM (Santos, 2002).

Modelos cineticos para o processo de termoluminescencia

Modelo de Randall e Wilkins (cinetica de primeira ordem)

Randall e Willkins (1945) fizeram a primeira formulacao metematica do processo de TL, desprezando o re-armadilhamento de eletrons liberados termicamente.

A hipotese fundamental neste modelo e a probabilidade p, por unidade de tempo, de um eletron, num nivel de energia E, contado a partir do fundo de BC (Banda de Conducao), ser liberado da armadilha, a temperatura absoluta T:

$p = s.exp(- E/kT)$

(1.1),

onde K e a constante de Boltzmann, s e o fator de frequencia; E e tembem conhecido como o nome de energia de ativacao.

Supondo que os eletrons liberados termicamente recombinam-se com os buracos nos centros de recombinacao, imediatamente, a intensidade de emissao termoluminescente I(t) e proporcional a varicao do numero de armadilhas preenchidas com eletrons n, e temos

$I(t) \alpha -dn/dt = n.s.exp(- E/kT)$

(1.2)

Admitindo que o aquecimento da amostra e linear, com coeficiente linear $dT/dt = \beta$ contante positiva, obtemos a seguinte expressao para n(T):

$n(t) = n_o.exp\left(-\int_{T_o}^T \frac{s}{\beta}e^{-\frac{E}{kT'}}dT \right)$

(1.3)

onde $n_o = n(to)$ . Da equacao (1.2) obtem-se a seguite:

$I(T) = C.n_o.s.exp\left(-\frac{E}{kT}\right) exp\left(-\int_{T_o}^T \frac{s}{\beta}e^{-\frac{E}{kT'}}dT' \right)$

(1.4) .

A dependencia de $dn/dt$ em n conduz a cinetica de primeira ordem ou a cinetica monomolecular. Observamos umpico na emissao termoluminescente, cuja forma e assimetrica (colocar figura A)

Modelo de Garlick e Gibson (link) (cinetica de segunda ordem)

Na realidade, Garlick e gibson (1948), no seu trabalho original consideraram:

$I(t) = -C\frac{dn}{dt} = C\frac{n^2}{\tau}$

(1.5)

onde $\tau = p^{-1}$ e obtiveram a equacao da intensidade TL:

$I(T) = C.n^2_o\frac{s}{N}exp\left(-\frac{E}{kT}\right)\begin{bmatrix} 1 + \frac{n_os}{N\beta}\int^T_{To}exp\left(-\frac{E}{kT'} \right)dT' \end{bmatrix}^{-2}$

(1.6)

A presenca do temo $n^2$ na derivada de n em relacao ao tempo caracteriza a cinetica de segunda ordem ou cinetica bimolecular. surge um pico aproximadamente simetrico na emissao termoluminescente, como mostra a figura 2.2.B (FIGURA 2.2 B)

Modelo de Halperin e Braner

Um tratamento matematico generalizado e compreensivel fisicamente para o processo de TL foi feito por Halperin e Braner (colocar links para os nomes ) (1960), que utilizaram as equacoes diferenciais desenvolvidas em 1956 por Adirovich (link) para explicar o fenomero de fosforescencia(*) (rodape - a fosoforecencia pode ser considerada como termoluminescencia isotermica e pode dar similar informacao sobre os parametros das armadilhas). Halperin e Braner consideraram um modelo constando de uma unica especie de armadilha e uma de centros de recombinacao.

As N armadilhas estao ligadas a banda de conducao atraves de dois coeficientes: Um coeficiente de liberacao termica de eletrons aprisionados, p, e o outro de recaptura de eletrons livres, com n o numero de armadilhas preenchidas com eletrons e o de centros de recombinacao ocupadas com buracos, com m, a neutralidade da carga total e dada por:

$n + n_c = m$

(1.7)

As variacoes de n, nc e m em relacao ao tempo sao dadas por:

$\frac{dm}{dt} = -A_m.m.n_c$

(1.8)

$\frac{dn}{dt} = -s.n.exp\left(-\frac{E}{kT}\right)+ n_c\left(N-n\right)An$

(1.9)

$\frac{dn_c}{dt} = s.n.exp\left(-\frac{E}{kT}\right) - n_c\begin{bmatrix}mA_m + (N-n)A_n\end{bmatrix}$

(1.10)

A figura (X2) mostra o processo descrito pelas equacoes (1.8),(1.9) e (1.10). A intensidade de emissao termoluminescente e igual a taxa de variacao de m, isto e:

$I(t) = -C\frac{dm}{dt}$

(1.11)

A primeira equacao descreve o processo no qual a concentracao m varia com t por consequencia da recombinacao de eletron livre com buraco (FIGURA 2.3)

A segunda equacao descreve a cinetica de eletrons entre as armadilhas e a banda de conducao. A taxa de liberacao desses eletrons e proporcional a concentracao de eletrons aprisionados n, e a probabilidade p, e a taxa de recaptura e proporcional a concentracap de n com t e, por isso, descrita pela equacao (1.9). A terceira equação descreve a variacao de $n_c$ com t e, e claro, depende de eletrons liberados das armadilhas, $n.s.exp\left(-\frac{E}{kT}\right)$ , de elétrons recapturados $A_n.n_c(N-n)$ e de eletrons que sobrem recombinacao $A_mn_cm$ .

É necessário acrescentar a condicao de neutralidade global de carga, ja mencionada (eq 1.7). Tomando a primeira derivada de m com respeito a tempo, tem-se:

$\frac{dm}{dt} = \frac{dn}{dt}+\frac{dn_c}{dt}$

(1.12)

O conjunto das equações (1.8)-(1.10), pode ser resolvido numericamente para o conjunto de parametros $A_m, A_n, n_o, m_o, n_c, N, E e s$ , (Shenker e Chen, 1972) (link).

As hipoteses basicas adotadas por Adirovitch (link), Halperin e Braner (link), sao as seguintes:

$|\frac{dn_c}{dt}| << |\frac{dn}{dt}|$

(1.13)

$n_c << n$

(1.14)

A primeira hipotese significa que nao ocorre uma acumulacao de eletrons na banda de conducao, portanto, a equacao (1.12), torna-se:

$\frac{dm}{dt}\approx \frac{dn}{dt}$

(1.15)

A segunda hipotese significa que durante o aquecimento da amostra, a concentracao de eletrons na banda de condução e muito menor que a de armadilhas cheias. A partir das hipoteses dadas na equação (1.13) e (1.14), e das equações (1.8) - (1.11), obtemos a seguinte relação:

$I = -\frac{dm}{dt} = \frac{s.n.exp\left(- \frac{E}{kT}\right)A_mm}{A_mm+A_n(N-n)}$

(1.16)

Esta e uma equacao geral da intensidade de emissao termoluminscente e pode ser usada para os casos particulares dos processos de cineticas de primeira e segunda ordem, adicionadas algumas hipoteses.

No caso de:

$A_mm >> A_n(N-n)$

(1.17)

a equacao (1.16) torna-se

$I = -\frac{dn}{dt}=s.n.exp\left(-\frac{E}{kT}\right)$

(1.18)

que corresponde ao modelo proposto por Randall e Wilkins e e igual a equacao (1.2)

Considere o caso contrario, isto e,

$A_n(N-n) >> A_M$

(1.19) .

Como n e m diminuem durante o aquecimento da amostra, a relacao acima continua sendo valida, uma vez que essa relacao e satisfeita inicialmente. Alem disso, se N >> n, a equacao (1.16) torna-se

$I = -\frac{dn}{dt}= \left(\frac{s.A_m}{N.A_n}\right)n.m.exp\left(-\frac{E}{kT}\right)$

(1.20)

Considerando 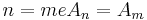$n = m e A_n = A_m$ , a equacao (2.20) fica:

$I = \left(\frac{s}{N} \right)n^2exp\left(-\frac{E}{kT}\right)$

(1.17)

que corresponde a equacao de segunda ordem deduzida por Garlick e Gibson (link).

Aplicações

nuclear e medical applications

Geologia e archeologi

Wulfenita apresenta fluorescência quando resfriada a baixo de zero

Termoluminescência da Fluorita, que apresenta o tom azulado quando é aquecida

Referências

Radiation Measurements Volume 35, Issue 1, January 2002, Pages 47–57
Dissertação de Mestrado - 2001 - Andrade, Marcelo Barbosa de - Datação de Peixe Fóssil da Chapada de Araripe-CE por Termoluminescência e Ressonância Paramagnética Eletronica (EPR)
Dissertação de Mestrado - 1994 - Arenas, Jorge Sabino Ayala - Datação de sedimento da Ilha de Cananéia, SP, e da Duna de Pilão Arcado, Bahia, pelo método de termoluminescência.

McKeever, S.W.S. Thermoluminescence of Solids
Thermo1
Thermo2
wiki - Ing
- Thermoluminescence pdf

@@ Linha 136: / Linha 136: @@
 |-----
 | bgcolor="#fff8ff" |<math> I(t) = -C\frac{dm}{dt}</math>
-|}(1.12) </center>
+|}(1.11) </center>
@@ Linha 143: / Linha 143: @@
-A segunda equacao descreve a cinetica de eletrons entre as armadilhas e a banda de conducao. A taxa de liberacao desses eletrons e proporcional a concentracao de eletrons aprisionados n, e a probabilidade p, e a taxa de recaptura e proporcional a concentracap de n com t e, por isso, descrita pela equacao (2.9).
+A segunda equacao descreve a cinetica de eletrons entre as armadilhas e a banda de conducao. A taxa de liberacao desses eletrons e proporcional a concentracao de eletrons aprisionados n, e a probabilidade p, e a taxa de recaptura e proporcional a concentracap de n com t e, por isso, descrita pela equacao (1.9).
-a terceira equacao descreve a variacao de nc com t e, e claro, depende de eletrons liberados das armadilhas, <math> </math>, de eletrons recapturados <math> </math> e de eletrons que sobrem recombinacao <math> </math>.
+A terceira equação descreve a variacao de <math> n_c </math> com t e, e claro, depende de eletrons liberados das armadilhas, <math> n.s.exp\left(-\frac{E}{kT}\right) </math>, de elétrons recapturados <math>A_n.n_c(N-n) </math> e de eletrons que sobrem recombinacao <math> A_mn_cm </math>.
-E necessario acrescentar a condicao de neutralidade global de carga, ja mencionada (eq 2.7). Tomando a primeira derivada de m com respeito a tempo, ten-se:
+É necessário acrescentar a condicao de neutralidade global de carga, ja mencionada (eq 1.7). Tomando a primeira derivada de m com respeito a tempo, tem-se:
-<math> </math>
+<center>
+{| border=1 cellpadding=10 style="border-collapse:collapse"
+|-----
+| bgcolor="#fff8ff" |
+<math> \frac{dm}{dt} = \frac{dn}{dt}+\frac{dn_c}{dt} </math>
+|}(1.12) </center>
-O conjunto das equacoes (2.8) - (2.10), pode ser resolvido numericamente para o conjunto de parametros Am, An, no, mo, nc, N, E e s, (Shenker e Chen, 1972) (link).
+O conjunto das equações (1.8)-(1.10), pode ser resolvido numericamente para o conjunto de parametros <math>A_m, A_n, n_o, m_o, n_c, N, E e s </math>, (Shenker e Chen, 1972) (link).
 As hipoteses basicas adotadas por Adirovitch (link), Halperin e Braner (link), sao as seguintes:
+<center>
+{| border=1 cellpadding=10 style="border-collapse:collapse"
+|-----
+| bgcolor="#fff8ff" |
+<math> |\frac{dn_c}{dt}| << |\frac{dn}{dt}| </math>
+|}(1.13) </center>
-<math> </math> <math> </math>
+<center>
+{| border=1 cellpadding=10 style="border-collapse:collapse"
+|-----
+| bgcolor="#fff8ff" |
+<math> n_c << n </math>
+|}(1.14) </center>
-A primeira hipotese significa que nao ocorre uma acumulacao de eletrons na banda de conducao, portanto, a equacao (2.12), torna-se:
-<math> </math>
-A segunda hipotese significa que durante o aquecimento da amostra, a concentracao de eletrons na banda de conducao e muito menor que a de armadilhas cheias.
+A primeira hipotese significa que nao ocorre uma acumulacao de eletrons na banda de conducao, portanto, a equacao (1.12), torna-se:
-A partir das hipoteses dadas na equacao (2.13) e (2.14), e das equacoes (2.8) - (2.11), obtemos a seguinte relacao:
+<center>
+{| border=1 cellpadding=10 style="border-collapse:collapse"
+|-----
+| bgcolor="#fff8ff" |
+<math> \frac{dm}{dt}\approx  \frac{dn}{dt} </math>
+|}(1.15) </center>
+A segunda hipotese significa que durante o aquecimento da amostra, a concentracao de eletrons na banda de condução e muito menor que a de armadilhas cheias.
+A partir das hipoteses dadas na equação (1.13) e (1.14), e das equações (1.8) - (1.11), obtemos a seguinte relação:
+<center>
+{| border=1 cellpadding=10 style="border-collapse:collapse"
+|-----
+| bgcolor="#fff8ff" |
+<math> I = -\frac{dm}{dt} = \frac{s.n.exp\left(- \frac{E}{kT}\right)A_mm}{A_mm+A_n(N-n)} </math>
+|}(1.16) </center>
-<math> </math>
 Esta e uma equacao geral da intensidade de emissao termoluminscente e pode ser usada para os casos particulares dos processos de cineticas de primeira e segunda ordem, adicionadas algumas hipoteses.
-No caso de: <math> </math>
+No caso de:
+<center>
+{| border=1 cellpadding=10 style="border-collapse:collapse"
+|-----
+| bgcolor="#fff8ff" |<math>A_mm >> A_n(N-n) </math>
+|}(1.17) </center>
-a equacao (2.16) torna-se
+a equacao (1.16) torna-se
-.
-.
- <math> </math>
-que corresponde ao modelo proposto por Randall e Wilkins e e igual a equacao  (2.2)
+<center>
+{| border=1 cellpadding=10 style="border-collapse:collapse"
+|-----
+| bgcolor="#fff8ff" |<math>I = -\frac{dn}{dt}=s.n.exp\left(-\frac{E}{kT}\right) </math>
+|}(1.18) </center>
+que corresponde ao modelo proposto por Randall e Wilkins e e igual a equacao  (1.2)
-Considere o caso contrario, isto e, <math> </math>.
+Considere o caso contrario, isto e, <center>
+{| border=1 cellpadding=10 style="border-collapse:collapse"
+|-----
+| bgcolor="#fff8ff" |<math>A_n(N-n) >> A_M </math>
+|}(1.19) </center>.
-Como n e m diminuem durante o aquecimento da amostra, a relacao acima continua sendo valida, uma vez que essa relacao e satisfeita inicialmente. Alem disso, se N >> n, a equacao (2.16) torna-se
+Como n e m diminuem durante o aquecimento da amostra, a relacao acima continua sendo valida, uma vez que essa relacao e satisfeita inicialmente. Alem disso, se N >> n, a equacao (1.16) torna-se
-<math> </math>
+<center>
+{| border=1 cellpadding=10 style="border-collapse:collapse"
+|-----
+| bgcolor="#fff8ff" |<math>I = -\frac{dn}{dt}= \left(\frac{s.A_m}{N.A_n}\right)n.m.exp\left(-\frac{E}{kT}\right) </math>
+|}(1.20) </center>
-Considerando <math> </math>, a equacao (2.20) fica:
+Considerando <math> n = m e A_n = A_m </math>, a equacao (2.20) fica:
-<math> </math>
+<center>
+{| border=1 cellpadding=10 style="border-collapse:collapse"
+|-----
+| bgcolor="#fff8ff" |<math>I = \left(\frac{s}{N} \right)n^2exp\left(-\frac{E}{kT}\right)</math>
+|}(1.17) </center>
 que corresponde a equacao de segunda ordem deduzida por Garlick e Gibson (link).

Mudanças entre as edições de "Teced/textos/Grupo 5 13"

Edição das 22h19min de 11 de setembro de 2013

Conteúdo

Proposta

História

Modelos cineticos para o processo de termoluminescencia

Modelo de Randall e Wilkins (cinetica de primeira ordem)

Modelo de Garlick e Gibson (link) (cinetica de segunda ordem)

Modelo de Halperin e Braner

Aplicações

Referências

Ferramentas pessoais

Espaços nominais

Variantes

Visualizações

Ações

Pesquisar

Navegação

Imprimir/exportar

Ferramentas