NMR o que é? Como funciona?

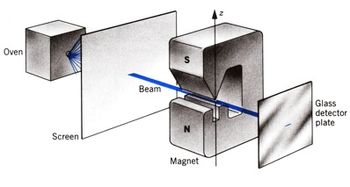
Na experiência de Stern-Gerlach, Figura 1, um feixe de prata vaporizada passa por uma região com campo magnético não uniforme e divide-se em dois formando a figura histórica reproduzida abaixo. Embora o feixe de átomos de prata seja eletricamente neutro, os átomos por possuírem um momento de dipolo magnético sofrem a ação do campo magnético não uniforme. Esta experiência demonstrou a quantização espacial prevista teoricamente por Wolfgang Pauli antes do desenvolvimento da mecânica ondulatória.

• 

  Figura 1: Arranjo experimental de Stern-Gerlach: observem o forno, de onde saem os átomos de Ag, um anteparo com uma pequena fenda para colimar o feixe, o ímã com pólos assimétricos e não uniformes para dar o campo magnético não uniforme, e, finalmente a placa detectora do feixe - Página 1080, Halliday Resnick and Krane- Physics 4th edition Volume 2 Extended.1992 , John Wiley& Sons.

• 

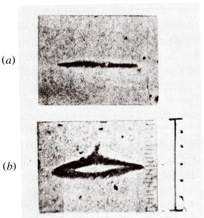
  Figura 2: resultados da experiência de Stern-Gerlach, onde se vê deposito de Ag sobre a placa de vidro, que é usada como detector do feixe. Em (a) campo magnético desligado, e, em (b) campo magnético ligado mostrando o feixe partido em dois. A barra vertical mostrada à direita na figura representa 1 mm - Página 1081, Halliday Resnick and Krane- Physics 4th edition Volume 2 Extended.1992 , John Wiley& Sons.

O momento de dipolo magnético μ está associado ao momento angular orbital L, ambas grandezas são vetoriais, sendo L o momento angular orbital relativo ao elétron orbitando, o que, por sua vez, corresponde a uma minúscula argola de corrente. A fim de resolver o problema do átomo de hidrogênio na teoria de Bohr são necessários três números quânticos n - número quântico principal, l - número quântico orbital e ml número quântico magnético.

Símbolo	Nome	Associado a uma	Valores permitidos
n	número quântico principal	energia , raio médio	1, 2, 3...
l	número quântico orbital	momento angular orbital	0, 1, 2...., n-1
ml	número quântico magnético	direção do momento angular orbital	0, ±1, ±2,....±l

Na figura abaixo estão mostradas as possíveis orientações do vetor momento angular , para l= 1, 2 e 10.As escalas utilizadas foram arbitrariamente escolhidas para efeito de ilustração dos possíveis valores das projeções ml .

Arquivo:X.jpg

Figura 3: Valores permitidos para alguns exemplos de L, Lz são as projeções do momento angular orbital, sendo ml a projeção no eixo z, mostrando apenas os valores permitidos da projeção. Foi usada uma escala para cada valor de l.

A experiência de Stern – Gerlach demonstra claramente que o vetor momento magnético de um átomo pode assumir um número finito de direções discretas no espaço, o que não é previsto na teoria clássica. Na ilustração33 fica claro que podem existir sempre um número impar de projeções possíveis , se o momento angular for l são possíveis 2l+1 projeções. Entretanto na experiência de Stern Gerlach o feixe se divide em dois, o que representa um valor de l=1/2 o que não era previsto até então. Wolfgang Pauli teoricamente mostrou a necessidade de introduzir um novo número quântico para o elétron no átomo com os valores 1/2 e -1/2 . Dois alunos de pós-graduação, Samuel Goudsmit e George Uhlenbeck propuseram a noção de spin do elétron como a interpretação do número quântico então recentemente proposto por Pauli. O spin do elétron é freqüentemente chamado de momento angular intrínseco e associado figurativamente (embora não seja correto) ao movimento de rotação de uma partícula sobre o seu eixo. O valor assumido pelo spin do elétron é sempre 1/2 qualquer que seja o seu estado de movimento, diferentemente do momento angular orbital que pode assumir diferentes valores. O spin do elétron pode ser representado por um vetor de magnitude:

$S=\frac{S(S+1)^{(\frac{1}{2})}}{\hbar}$

A componente desse vetor no eixo z pode ser escrito como

$S_{z}=m_{s}\hbar$

Assim como no caso do momento angular orbital L as componentes permitidas de S diferem de uma unidade, de modo que os valores possíveis de ms são:

$m_{s}=\pm \frac{1}{2}$

Associado ao momento angular de spin existe o momento magnético μs

$\mu_s=-\frac{e}{m_e}S$,

onde μs e S são na verdade grandezas vetoriais assim como L e μ, anteriormente definidos, e devem ser assim consideradas ( isto é tem módulo, direção e sentido). Os números quânticos para o momento angular orbital l e sua projeção ml aparecem naturalmente na resolução da equação de Schrödinger para o átomo de hidrogênio. O momento angular de spin e sua projeção ms foram devidamente introduzidos pelo físico matemático inglês A. M. Dirac na resolução do átomo de hidrogênio com correções relativísticas aplicadas ao problema não relativístico resolvido através da equação de Schrödinger, com a introdução de um novo número quântico, o quarto número, o spin do elétron s=1/2ħ.

Figura 4: – A fotografia mostra Wolfgang Pauli (à esquerda) e Niels Bohr observando um pequeno pião de festinha infantil, que gira, gira numa direção e de repente vira de cabeça para baixo. Eles aguardam o “spin flip” do pião!

Assim podemos finalmente explicar a subdivisão do feixe da experiência de Stern-Gerlach. Também esse conceito é usado para explicar a ressonância magnética nuclear. Como se sabe tanto o próton como o nêutron tem spin 1/2e tem momento magnético μ, que causa um desdobramento dos níveis de energia quando sob ação de um campo magnético B, com ΔE = 2μsB.

É exatamente essa diferença de energia que aparece quando ocorre um “spin flip”, isto é , uma mudança do spin do próton de +1/2 para -1/2. Essa é a base dos exames de ressonância magnética!

Materiais orgânicos são formados de muitos átomos de hidrogênio, que quando submetidos a um campo magnético intenso podem sofrer o “spin flip”, que causa uma absorção de energia da fonte de radio-freqüência, que produz o campo magnético intenso dos aparelhos. Essa informação (de absorção de energia) é processada com programas adequados de computação pesquisando previamente vários materiais como básicos para a análise conveniente das medições de absorção gravadas no decorrer de cada exame. Para moléculas orgânicas essa região de freqüência RF é a adequada para análises. Na figura 5 está mostrado um espectro da energia absorvida em função do campo magnético aplicado B usando como prova a amostra de etanol, que é formado por : CH3 – CH2 - OH , onde CH3 é o radical metila, CH2 é o radical metileno. Dependendo da forma como os prótons se acoplam alinhados paralelamente ou antiparalelamente ao campo externo aplicado pode haver diferentes valores de energias absorvidas. No corpo humano em cada tipo de estrutura existente como osso, músculo, nervo etc o hidrogênio está “ligado” de forma diferente. Assim o “spin flip” se dará com diferentes valores de campos magnéticos. Faz se o acúmulo das informações obtidas em varreduras do feixe magnético através do membro a ser estudado, o que possibilita a análise das exposições sobrepostas armazenadas num computador. Por computação essas estruturas examinadas são transformadas em imagens correspondentes.

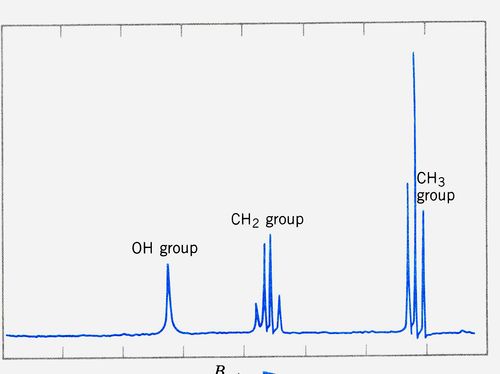
Figura 5: – Espectro de energia absorvida pelo etanol num campo magnético que varia de $10^{-4}$ T na escala horizontal mostrada na figura. A identificação dos grupos de picos está indicada na figura. No uso da NMR para exames diagnósticos tem ainda uma vasta gama de computação gráfica envolvida.