O que é SPIN?
Conteúdo[ocultar] |
Espectroscopia e o spin do núcleo
O estudo da espectroscopia, muito difundido no século XIX, permitia a identificação confiável de materiais pelos espectros emitidos. Muitos detalhes dos modelos atômicos foram desenvolvidos através da análise detalhada dos espectros ópticos de vários elementos. O modelo do átomo como um núcleo central pesado circundado por elétrons na eletrosfera foi testado de diversas formas e tem mostrado coerência ao longo do tempo. As principais características apresentadas pelos átomos, assim como conhecidos desde o final do século XIX, são reproduzidas pela teoria quântica. Entende-se que as elaborações das teorias têm que ser adequadas na reprodução das medidas experimentais, feitas com precisão cada vez maior. A espectroscopia desenvolveu-se até atingir a resolução necessária para se detectar linhas espectrais muito próximas. É o caso do estudo das linhas de “fine splitting” desdobramento fino do espectro. Sob ação de um campo magnético pode haver a decomposição de um estado em sub-estados dando origem a dubletos, a tripletos ou a quadrupletos com comprimentos de onda bem próximos. Pode ainda existir o “hiperfine splitting” (desdobramento hiper-fino) com linhas espectrais desdobradas em várias linhas muito próximas, também em presença de campos magnéticos, que são conhecidas como linhas da estrutura hiperfina. Nesse caso o spin do núcleo afeta os níveis de energia atômicos dando origem à estrutura hiperfina.
Ao longo do tempo, modificações das teorias vigentes foram incorporadas para explicar os espectros conhecidos, conforme ficavam disponíveis espectros com melhor resolução, isto é, mostrando desdobramentos até então desconhecidos nos espectros: uma linha podia ser desdobrada em várias com o desenvolvimento de melhores espectroscópios. Teóricos contribuíram muito propondo muitas vezes aspectos inusitados, como o spin, dando novas interpretações a fenômenos já conhecidos e que redundavam em novas propriedades dos átomos ou dos núcleos conhecidos. O spin do núcleo foi o que Pauli, em 1924, propôs como uma nova propriedade do núcleo atômico para explicar as evidências experimentais de espectros ópticos de alta resolução. Estudos sistemáticos mostravam que deveria haver alguma propriedade nuclear importante desconhecida afetando os níveis de energia de forma a dar os novos resultados experimentais. Logo o conceito de spin foi atribuído também para os elétrons, para os quais é até mais fácil de visualizar. Como os elétrons giram em torno do núcleo pode se atribuir um momento angular orbital l e um spin intrínseco s, este poderia ser comparado a um movimento de rotação em torno de um eixo que passa por ele mesmo e o outro referente à órbita. Conhecemos como sendo de Stern e de Gerlach a experiência (1921) decisiva da existência do momento angular, incluindo uma quantização espacial na teoria de Bohr. As órbitas da teoria de Bohr devem ter um momento angular que seja um múltiplo inteiro h/2π que é lh/2π, sendo l um número inteiro e h a constante de Planck. Refinamentos à teoria quântica segundo Bohr, Sommerfeld e outros requerem a quantização, não só dos momentos angulares, mas também das componentes numa direção definida. Essas componentes devem ter valores mh/2π onde m é um número inteiro e positivo ou negativo, que seja menor que a magnitude de l. Disso segue que um átomo só pode ter certas orientações no espaço. Por exemplo, se l =1, m pode ter valores -1, 0, +1. Uhlenbeck e Goudsmit dois físicos holandeses descobriram (em 1925) que o elétron não pode ser considerado como se fosse uma carga elétrica pontual, mas que fosse uma pequena esfera que tenha um spin um momento angular intrínseco. Como se espera, o spin deve estar ligado ao valor h/2π, mas o que diferia é que o spin intrínseco tem o valor que é a metade disso 1/2 h/2π. Depois de resistir à desconfiança de teóricos famosos, finalmente a descoberta foi aceita. ( Segré-op. cit., pág.137-141).
SPIN do PRÓTON e do NÊUTRON
(Adaptado do livro “Nuclear Physics”, I. Kaplan, Addison Wesley, Reading Massachusetts, USA, 1956. cap. 8 seção 8.5) O próton e o nêutron no núcleo têm um momento angular que pode ser atribuído ao movimento de rotação da partícula em torno de um eixo que passa através do seu centro de massa. A magnitude desse momento angular de spin é 1/2ħ, ou seja, 1/2 (h/2π). As propriedades quânticas de um momento angular desse tipo são tais que a sua orientação no espaço pode ser descrito apenas por dois estados: o eixo do spin “paralelo” ou “anti-paralelo” a uma dada direção. A componente do spin ao longo de uma direção, por exemplo, o eixo z, pode ser ou +1/2ħ ou –1/2ħ. Além do spin intrínseco, a cada nucleon (um próton ou um nêutron) pode ser atribuído um número quântico relativo ao seu movimento orbital dentro do núcleo, o momento angular orbital l. De acordo com a teoria quântica, o momento angular orbital é um vetor cujo componente maior possível em qualquer direção dada é um múltiplo inteiro de h/2π. Cada nucleon tem um momento angular total i dado por:
onde l é o momento angular orbital e s é o momento angular de spin. O spin de cada nucleon pode ser obtido ao somar ou subtrair 1/2ħ dependendo da sua orientação com relação ao eixo de referência, e assim i é semi-inteiro. (Note que em geral se chama spin tanto o spin intrínseco s como o momento angular total i. Em alguns livros o momento angular total é denominado j. O termo spin i , conforme o autor se refere ao spin total de um núcleo e em outros casos usam I letra maiúscula, para indicar o spin total.) Para o caso de mais que um nucleon no núcleo são usadas letras maiúsculas para os momentos angulares do núcleo:
onde L é o momento angular orbital total, e S o momento angular de spin total. O momento angular total é um vetor representado por I, e a quantidade escalar I é definida como o máximo valor possível da componente de I em qualquer direção dada. O momento angular orbital L é um múltiplo inteiro de ħ; S é um múltiplo par de 1/2ħ se o número de partículas for par, e um múltiplo impar de 1/2ħ se o número de partículas for ímpar. Dessa forma I é um múltiplo inteiro de ħ quando A é par, e um múltiplo impar de semi-inteiro quando A é ímpar, de acordo com os dados experimentais. Finalmente, para os diferentes valores de l são atribuídas letras:
- s para l=0,
- p para l=1,
- d para l=2 ,
e etc., que é a nomenclatura usada para os elétrons.
Outra vez o decaimento Beta : os spins
Este texto se refere ao decaimento beta de alguns nuclídeos como 32P,137Cs, 60Co. Estes nuclídeos são emissores beta e gama com exceção do fósforo 32,que é só emissor beta. Os demais Cs e Co decaem para estados excitados do núcleo filho e decaem logo em seguida por emissão gama ao estado fundamental do núcleo resultante.
No decaimento beta sabe-se que um nêutron decai num próton + um elétron e mais um antineutrino. Mas antes de saber da existência do neutrino, se um núcleo A emite um elétron (que é o beta-) e se transforma num núcleo B, por conservação de energia, a energia do elétron deveria ser bem determinada, o que não é observado experimentalmente.
O espectro de energia do beta é um espectro contínuo desde zero até uma energia máxima. Pode-se obter esse espectro usando detectores proporcionais, que são detectores a gás que funcionam não na região Geiger, mas na região proporcional. Um detector proporcional, é um detector a gás em baixa pressão, normalmente se usa o gás conhecido como P10 (pe dez), uma mistura de argônio e isobutano (em pressão baixa de alguns militor). A altura do pulso produzido pela ionização primária e posterior multiplicação é proporcional à energia da partícula ionizante e chega a ser de alguns milivolts (milivolt= 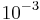 V). Dessa forma são necessários equipamentos específicos para a amplificação e análise eletrônica dos pulsos. Uma fonte beta emissora tem uma distribuição de altura de pulsos desde zero até uma energia máxima o que pela conservação de energia e de quantidade de movimento não pode ser explicado sem a presença de uma terceira partícula no decaimento.
Outras quantidades que devem ser conservadas num decaimento β estão satisfeitas, pois a carga está conservada.
Quanto ao spin, o momento angular total também tem que ser conservado.
O nêutron tem spin ½, o próton e o elétron também tem spin ½, são todos férmions.
Os spins são compostos, ou seja, são acoplados de uma forma muito especial, como se fossem vetores paralelos ou antiparalelos; dessa forma dois spins paralelos de ½ cada somam para dar spin 1 e dois spins antiparalelos de ½ cada dá spin zero.
Assim sendo, se um nêutron decaisse para um próton +um elétron ½ → ½ + ½ seria possível obter spins 0 ou 1 e não o ½ do nêutron.
Assim para que haja conservação do spin também deve haver outra partícula, o neutrino, que também tem spin ½ .
Agora três partículas de spin ½ podem se acoplar para dar desde spin 3/2 até ½. Dessa forma a conservação está contemplada:
V). Dessa forma são necessários equipamentos específicos para a amplificação e análise eletrônica dos pulsos. Uma fonte beta emissora tem uma distribuição de altura de pulsos desde zero até uma energia máxima o que pela conservação de energia e de quantidade de movimento não pode ser explicado sem a presença de uma terceira partícula no decaimento.
Outras quantidades que devem ser conservadas num decaimento β estão satisfeitas, pois a carga está conservada.
Quanto ao spin, o momento angular total também tem que ser conservado.
O nêutron tem spin ½, o próton e o elétron também tem spin ½, são todos férmions.
Os spins são compostos, ou seja, são acoplados de uma forma muito especial, como se fossem vetores paralelos ou antiparalelos; dessa forma dois spins paralelos de ½ cada somam para dar spin 1 e dois spins antiparalelos de ½ cada dá spin zero.
Assim sendo, se um nêutron decaisse para um próton +um elétron ½ → ½ + ½ seria possível obter spins 0 ou 1 e não o ½ do nêutron.
Assim para que haja conservação do spin também deve haver outra partícula, o neutrino, que também tem spin ½ .
Agora três partículas de spin ½ podem se acoplar para dar desde spin 3/2 até ½. Dessa forma a conservação está contemplada:
Spin e o modelo atômico
Adaptado de “Nuclear Physics”, I. Kaplan, Addison Wesley, Reading Massachusetts, USA, 1956. (Cap 8 seção 8.2) No final do século XIX, pesquisavam-se muito os espectros emitidos pelos diferentes átomos. Muito do que se conhece hoje como física moderna se deve a essa área do conhecimento, a espectroscopia. A constatação de que as massas dos elementos eram bem próximas de números inteiros corroboravam a idéia que os elementos devem ser formados por unidades básicas. A existência de elementos com massas diferentes, que hoje conhecemos como os isótopos de um elemento já eram conhecidos. Por exemplo, os isótopos radioativos do chumbo com números de massa 214, 212, 211 e 210 assim como três não radioativos de pesos atômicos 206, 207 e 208 foram introduzidos para explicar espectros observados. Por outro lado, o conhecimento das partículas α e das partículas β emitidas por alguns átomos de elementos radioativos levou à hipótese que prótons e elétrons existiam dentro do núcleo. Assim, surgiu o modelo do átomo constituído por prótons e elétrons, sendo o núcleo formado por prótons e elétrons em número adequado para dar conta da carga e massa já determinadas. O estudo detalhado, com boa resolução, de espectros emitidos por diferentes átomos, mostra que uma linha espectral se desdobra em várias linhas muito próximas umas das outras. Essa estrutura hiperfina não podia ser explicada através do modelo atômico vigente. Pauli em 1924 admitiu que essa estrutura estaria relacionada a uma propriedade até então desconhecida do núcleo atômico, o spin do núcleo, isto é, o núcleo atômico deve ter um momento angular associado a um momento magnético, responsável pelo “splitting” das linhas espectrais verificadas experimentalmente. As propriedades associadas com a estrutura hiperfina do átomo são a massa e o momento angular do núcleo. Na figura abaixo, em (a) está mostrado o espectro de um gás sem campo magnético, e em (b) o desdobramento das linhas pela presença do campo magnético.
Os espectros atômicos podem ser explicados através de expressões relativamente simples onde entra uma constante denominada constante de Rydberg. Essas expressões podem ser derivadas através da teoria de Bohr. Moseley foi um dos cientistas que realizaram muitos experimentos importantes da época. A constante de Rydberg devia ser ligeiramente corrigida, para dar conta do movimento relativo do núcleo e dos elétrons ao seu redor, para reproduzir os espectros de diferentes isótopos de um elemento químico. Entretanto havia casos em que apenas esses ajustes da constante não eram suficientes. O momento angular de um núcleo pode ter diferentes valores para núcleos diferentes e também para diferentes isótopos de um mesmo elemento. Assim, o momento angular, o spin, de um núcleo pode ser determinado através da análise dos seus espectros de estruturas hiperfinas. Os spins de núcleos com número de massa ímpar são múltiplos semi-interiros de ħ ( ħ= h/2π e h é a constante de Planck). Os spins de núcleos com número de massa par são zero ou múltiplos inteiros de ħ. O spin do núcleo é representado em geral por I e o spin nuclear é dado por I.ħ, onde I = 0,1,2,3,... para A par e I = 1/2, 3/2, 5/2 ... para A impar. O spin foi atribuído também aos elétrons, cada elétron tem spin 1/2.ħ.
O nitrogênio como tem massa 14 e carga 7, no modelo falho, teria então 7 elétrons girando ao redor de um núcleo com 14 protons e 7 elétrons, portanto teria 21 partículas de spin ½ cada, o que resulta num spin semi inteiro, não compatível com as observações experimentais de estrutura hiperfina. O spin do nitrogênio é 1, o que foi explicado com a aceitação da existência do nêutron, que como o próton deve ter spin 1/2ħ o núcleo do nitrogênio é formado por 7 prótons e 7 nêutrons.

