Teced/textos/Grupo 2
Conteúdo[ocultar] |
FÍSICA EXPERIMENTAL - O EFEITO FOTOELÉTRICO
Introdução Teórica
O efeito fotoelétrico consiste no fenômeno de extrair elétrons da superfície de metais através da incidência de radiação eletromagnética. Assim, as ondas eletromagnéticas fornecem energia para o elétron sobre o qual incidem que por sua vez tem um incremento de energia cinética podendo “escapar” do material que o continha. Este efeito foi descoberto por Heinrich Hertz em 1887 e é uma das formas de se extrair elétrons de um material, sendo as outras formas a emissão termoiônica, a emissão secundária e a emissão de campo, sendo que essas últimas não serão discutidas no presente experimento. Para melhor compreensão desta fenomenologia foram realizados diversos experimentos no inicio do século de 1900. Nestes experimentos algumas características foram observadas:
1. Que a energia cinética dos fotoelétrons é independente da intensidade de luz incidente;
2. Que a energia cinética máxima dos fotoelétrons de um determinado material depende somente da energia da luz incidente;
3. Que quanto menor a função-trabalho de um material emissor menor é a frequência limiar com que a luz consegue ejetar os elétrons;
4. E finalmente que o número de foto elétrons emitido é proporcional à intensidade da luz incidente.
No entanto, estas propriedades não podiam ser explicadas adequadamente com a teoria clássica do eletromagnetismo ondulatório, necessitando de novas considerações teóricas, sugeridas posteriormente pelo modelo teórico de Einstein. Einstein baseou-se na idéia de quantização de energia proposta por Planck através do estudo da radiação do corpo negro.
As ideias de Lenard
Lenard estudou os raios catódicos e foi responsável pelo descobrimento de diversas de suas propriedades. Resumidamente, quanto à emissão e geração dos raios catódicos (através do efeito fotoelétrico) ele observou que:
1 - No efeito fotoelétrico, a corrente elétrica (aqui entendida como quantidade de elétrons por unidade de tempo) medida é proporcional à intensidade da luz incidente.
2 - A energia cinética dos elétrons liberados é independente da intensidade da luz incidente, variando apenas com o comprimento de onda. Quanto maior o comprimento de onda, menor essa energia cinética e vice-versa.
O Modelo Teórico de Einstein para o Efeito Fotoelétrico
Em 1905, inspirado pela hipótese de Planck do quantum de ação, Einstein propôs que as ondas eletromagnéticas também seriam quantizadas, em unidades de energia hoje chamadas fótons e que einstein chamou de "os quanta de energia". A energia E de cada fóton seria dada por uma função da sua frequência υ e da constante de Planck h.
Desta forma, um elétron poderia absorver esta energia do fóton sendo capaz de ser ejetado da superfície de um material com energia cinética 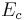 dada por:
dada por:
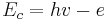 (I)
(I)
Onde h.v representa a energia do fóton incidente, e representa a carga do elétron, e φ a função trabalho do metal (portanto e.φ representa o trabalho para tirar um elétron da superfície do material). Definindo-se o potencial de freamento V0 como:
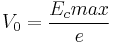 (II)
(II)
Obtemos a seguinte equação:
(III)
Com isso temos a explicação para a intensidade da fonte luminosa aumentar o número de fótons incidentes no tempo, logo aumentando o número de elétrons ejetado, porém não é determinante da energia com a qual o elétron é ejetado dependendo esta somente da frequência ν da luz da fonte. Também determina um potencial de corte de energia do fóton que se inferior à e.φ não é capaz de extrair um elétron.
Neste experimento então foi reproduzido o efeito fotoelétrico e suas observações diretas, também analisando a fenomenologia observada e mensurada através do modelo proposto por Einstein e suas propriedades.
Arranjo Experimental
Para o experimento foi optado por utilizar-se uma lâmpada de mercúrio (Hg) como fonte de luz, utilizando-se uma fenda, uma lente e uma rede de difração como filtros e seletores de comprimentos de onda específicos conforme o arranjo apresentado na figura 1.
Figura 1- Arranjo experimental onde 1 é a lâmpada de Hg, 2 a fenda, 3 a lente, 4 é a rede de difração e 5 a célula fotoelétrica.
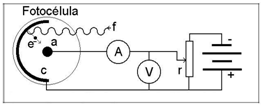
A luz incidente f após atingir a fotocélula revestida cilindricamente de um metal é capaz de arrancar elétrons da superfície do metal, atingindo o ânodo a. Esta fotocélula foi ligada a um voltímetro V e um pico-amperímetro A que por sua vez foram conectados à um ADC (analogic digital conversor), e à uma fonte de tensão constituída por baterias ligadas a um potenciômetro, conforme figura 2.
Figura 2- Arranjo experimental onde a luz incidente f remove o elétron e da superfície do metal.
O sinal do ADC então foi captado por um computador utilizando-se também uma fonte de tensão rampa, a qual fornece uma tensão de 0V a 4,5V que cresce linearmente com o tempo durante cerca de 40 segundos conforme a figura 3.
Figura 3- Arranjo experimental de aquisição digital das medidas.
A fonte rampa também possui uma chave inversora capaz de trocar a polaridade da tensão aplicada à foto célula. Com o sistema digital foram obtidas curvas de tensão por corrente, com as incertezas determinadas automaticamente por análise estatística de um conjunto de medidas obtido em um curto intervalo de tempo. Tivemos um problema de mal contato em algumas ligações dos fios do nosso arranjo experimental como mostrado na figura 4. Essas conexões com mal contato podem ter introduzido algumas variações nas nossas medidas, o que também pode ter contribuído para o distanciamento dos valores obtidos para os esperados teoricamente.
Métodos de Análise e Resultados
Para verificação experimental do efeito fotoelétrico e de suas propriedades foram adquiridas curvas de corrente por tensão utilizando uma fonte de luz de Hg e através do arranjo experimental descrito anteriormente foram selecionados os comprimentos de onda a serem analisados individualmente. Os comprimentos de onda do Hg analisados foram vermelho, amarelo, verde, azul e violeta com um filtro de intensidade permitindo passar próximo à 100% da luz. Todos os comprimentos de onda também foram analisados variando o filtro entre 100%, 80%, 60%, 40% e 20%. Também foram obtidas medidas sem incidência de luz para medir a corrente de fundo do arranjo experimental. Segundo o modelo teórico proposto por Einstein analisamos as curvas para a obtenção do potencial de corte V0 e levando em consideração que a corrente medida no arranjo experimental é representativa das somas da corrente produzida pelo efeito fotoelétrico desejado, pelo efeito fotoelétrico que ocorre no ânodo e pela corrente de fundo. As curvas obtidas forneceram o valor do potencial de corte após serem analisadas de três formas distintas.
O primeiro método foi para determinação do potencial de corte pela extrapolação da região crescente das curvas por uma reta, sendo o potencial de corte o ponto de intersecção desta curva com a abscissa.
O segundo método foi encontrar o valor no eixo das abcissas onde a corrente deixa de ser nula ou negativa.
E finalmente o terceiro método foi extrapolar uma reta na região crescente das curvas obtidas, e outra na região de corrente inversa, sendo a intersecção destas retas a estimativa do potencial de corte.
Primeiramente as curvas foram analisadas qualitativamente por observação de seus padrões e tendências.
Verificação das Idéias de Lenard
Aqui é evidenciado um caráter predominantemente qualitativo. O intuito foi comprovar os dois resultados dos trabalhos de Lenard:
1. no efeito fotoelétrico, a corrente elétrica (número de elétrons por unidade de tempo) medida é proporcional à energia carregada pela luz incidente e que
2. a energia cinética dos elétrons liberados é independente da energia da luz incidente, variando apenas com o comprimento de onda. Quanto maior o comprimento de onda, menor essa energia cinética e vice-versa.
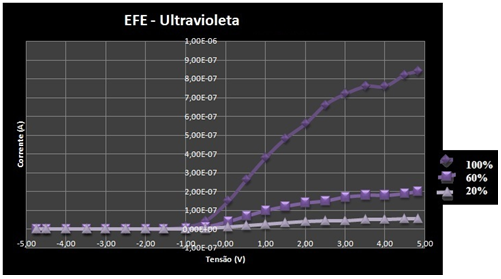
Para tanto, escolheu-se uma cor dentre o espectro luminoso e foram realizadas medições para diferentes intensidades. O gráfico com os resultados consolidados para o comprimento de onda correspondente ao ultravioleta com variação de intensidades de 100%, 60% e 20% é apresentado na figura 4.
Figura 4 – Corrente x Tensão para 3 intensidades diferentes no ultravioleta.
Calibração
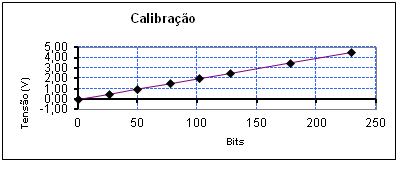
O programa de obtenção de dados não nos dava valores de tensão relacionados com as correntes medidas, porém os valores de tensão eram fornecidos em bits. Para a realizar as análises foi preciso fazer a conversão de bits para a tensão em volts. Isso visando obter a tensão de corte nos vários gráficos analisados. A partir do gráfico da figura 5 foi possível obter uma equação para a conversão de bits em volts.
Figura 5 – Calibração
Constante de Planck e Função Trabalho do Ânodo
Junto com os gráficos foram ajustadas retas a fim de com o coeficiente angular e o coeficiente linear se obter a constante de Planck e a função de trabalho do anodo, através da equação (III).
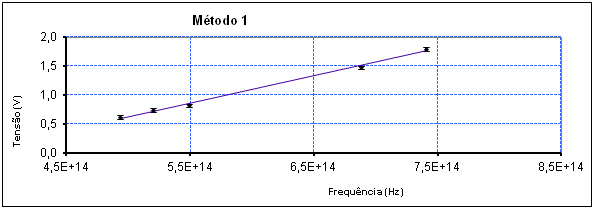
- A partir do  obtido pelo método 1
obtido pelo método 1
Figura 6 – Obtenção de h e φ pelo método 1.
h = (7,56) x [10^(-34)] J.s
V0 = 1,73 V
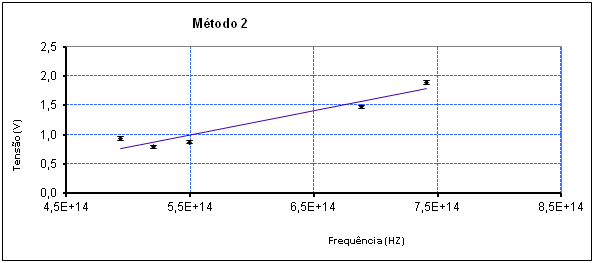
- A partir do V0 obtido pelo método 2
Figura 7 – Obtenção de h e φ pelo método 2.
h = (6,7) x [10^(-34)] J.s
V0 = 1,3 V
- A partir do V0 obtido pelo método 3
Figura 8 – Obtenção de h e φ pelo método 3.
h = (8,1) x [10^(-34)] J.s
V0 = 1,9 V
O valor da carga do elétron utilizada para os cálculos da constante de Planck foi: 1,6022 .[10^(-19)] C.
Discussão
Analisando os gráficos da seção 3.4 obtivemos as tensões de corte a fim de plotarmos os gráficos para a obtenção da constante de Planck e da função trabalho do anodo. Daí, através dos gráficos da tensão pela frequência obtivemos os valores para a constante de Planck para os três métodos citados anteriormente, dos quais somente a constante obtida pelo método 2 é compatível com o valor tabelado, o qual consideramos h = 6,626075 x [10^(-34)] Js.
Instantaneidade do efeito foto elétrico:
As observações realizadas anteriormente a tomada definitiva dos dados nos possibilitou verificar a instantaneidade da ocorrência do efeito fotoelétrico, que inicia-se assim que o cátodo é iluminado, não sendo mensurável qualquer atraso no efeito quando se obstruía e desobstruía a janela do cátodo.
Independência da intensidade luminosa no efeito fotoelétrico.
Através da análise da tensão de corte para diversas intensidades luminosas para a raia amarela e violeta podemos evidenciar a independência da intensidade luminosa para o valor do potencial de corte do modo esperado pelo modelo adotado.
Valores obtidos através dos ajustes:
Dos valores obtidos pelos diferentes métodos para a constante de Planck somente o do segundo método resultou em um valor compatível com o valor tabelado, os métodos 1 e 3 não são compatíveis com o valor tabelado, mesmo considerando a incerteza deste. Nós atribuímos esta discordância do método 2 com 1 e 3, devido a diferença no tipo da análise, o segundo permitia menos margem à influência do medidor no resultado que o primeiro, visto que nos dois métodos 1 e 3 a escolha dos pontos linearizados é feita visualmente tentando-se escolher a região que mais represente a reta de interesse, e o segundo método não dá esta liberdade de escolha a quem analisa os dados. As incertezas foram calculadas pela propagação de erros e pelo método dos mínimos quadrados.
Conclusão
As análises dos nossos resultados observando as curvas de corrente fotoelétrica versus tensão, permitiram a caracterização do efeito fotoelétrico, do qual foi verificado a instantaneidade, a dependência do potencial de corte com a frequência da radiação incidente, além da existência de correntes de fundo no anodo no circuito e devida a radiação de fundo proveniente principalmente da iluminação elétrica na sala do laboratório, as quais puderam ser tratadas convenientemente para a obtenção dos nossos resultados, a constante de Planck e a função trabalho do anodo. Apesar de somente o segundo método de análise ter resultado num valor compatível para a constante de Planck, isso não descarta a utilização dos outros métodos de análise. É necessário tornar mais preciso tais métodos reduzindo o fator humano neste processo, pois, de certa forma, a região de ajuste é escolhida de forma arbitrária.
Referências
S.T. Thornton, A. Rex - Modern Physics for Scientists and Engineers - 2nd Edition - Saunders College Publishing. Eisberg, Robert – Física quântica – Robert Eisberg e Robert Resnik – 29 Impressão – Elsevier Editora Ltda. J.H. Vuolo; Fundamentos da Teoria de Erros; Editora Edgard Blücher; 1981. Apostila FNC0377 – Laboratório de Física Moderna – Primeiro semestre de 2010 – Efeito Fotoelétrico. Site do Laboratório de Física Moderna 2012: http://disciplinas.stoa.usp.br/course/view.php?id=223