Mudanças entre as edições de "Teced/textos/Grupo 3"

De Stoa
< Teced‎ | textos
Ir para: navegação, pesquisa
(Criou página com '== We are doing it==')
 
Linha 1: Linha 1:
−
== We are doing it==
+
{{sem-fontes|data=Março de 2008}}
 +
{{Mecânica Clássica}}
 +
Na [[física]], '''velocidade''' relaciona a variação da posição no espaço em relação ao [[tempo]], ou seja, qual a distância percorrida por um corpo num determinado intervalo temporal. É uma [[grandeza vetorial]], possuindo [[direção]], [[sentido (matemática)|sentido]] e [[módulo]], esse último chamado de [[rapidez]] e de dimensões [L][T]<sup>-1</sup>, sendo medida no SI em metros por segundo (m/s ou ms<sup>-1</sup>). Em geral, os símbolos da velocidade são '''v''' ou <math>\vec{v}</math>, o primeiro para a [[velocidade escalar]] e o segundo para o vetor velocidade.
 +
A variação da velocidade em relação ao tempo é a [[aceleração]].
 +
 
 +
== Equações de velocidade ==
 +
Velocidade é um conceito fundamental para a [[mecânica clássica]]. Foi a partir desse que os primeiros físicos puderam desenvolver o estudo do movimento dos corpos, tornando-se capazes de descrever trajetórias através de funções matemáticas. [[Isaac Newton]], pai da mecânica clássica, desenvolveu o [[cálculo diferencial]] a partir desse estudo.
 +
Há dois tipos de movimentos considerados mais simples: o movimento retilíneo uniforme(MRU) e o movimento retílineo uniformemente variado(MRUV), que são representados por equações lineares e quadrádicas respectivamente.
 +
Para outros tipos de movimento mais complexos utiliza-se a derivada.
 +
 
 +
=== Movimento Retílineo Uniforme ===
 +
É o movimento descrito por objetos com velocidade constante, para tal, é preciso que a resultante das forças que atuam sobre o corpo seja nula. Dado um deslocamento <math>\Delta s</math>, em um tempo <math>\Delta t</math> A velocidade escalar '''v''' é dada por:<br />
 +
<math>\mathbf{v}=\frac{\Delta s}{\Delta t}</math>.<br />
 +
Somente no MRU a velocidade de um corpo a qualquer instante é igual à sua velocidade média.
 +
A equação do espaço '''S''' em função do tempo '''t''', a partir de um ponto '''<math>S_o</math>''' é:<br />
 +
<math>S=S_o+\mathbf{v}t</math><br /><br />
 +
O gráfico <big>s</big>x<big>t</big> desse movimento é uma linha reta cuja tangente do ângulo de inclinação dessa reta, em relação ao eixo '''t''' é o valor da velocidade.
 +
 
 +
=== Movimento Retilíneo Uniformemente Variado ===
 +
É o movimento de objetos que variam sua velocidade de forma constante, ou seja, possuem [[aceleração]] constante.
 +
No MRUV a equação da aceleração é análoga à da velocidade no MRU; e a equação de velocidade no MRUV é análoga à do espaço no MRU.<br />
 +
<math>a=\frac{\Delta \mathbf{v}}{\Delta t}</math><br />
 +
 
 +
<math>\mathbf{v}=\mathbf{v}_o+at</math><br />
 +
E a equação do espaço é a seguinte:<br />
 +
<math>S=S_o+\mathbf{v}_ot+\frac{at^2}{2}</math><br />
 +
O gráfico <big>s</big>x<big>t</big> desse movimento é uma parábola.
 +
 
 +
Veja mais em [[movimento retilíneo]].
 +
 
 +
=== [[Derivada]] ===
 +
Os dois movimentos acima só ocorrem em condições muito especificas, para estudar os movimentos dos corpos como ocorrem na natureza Newton desenvolveu a derivada, para calcular a velocidade instantânea de um corpo em certo instante é necessário usar [[limite]], medindo-se uma variação infinitesimal de espaço em um intervalo infinitesimal de tempo.<br />
 +
<math>\mathbf{v}=\lim_{\Delta t \rightarrow 0}\frac{\Delta s}{\Delta t}=\frac{ds}{dt}</math><br />
 +
Da definição de derivada:<br />
 +
<math>\mathbf{v}=\frac{ds}{dt}=\lim_{\Delta t \rightarrow 0}\frac{S\left(t+\Delta t\right)-S(t)}{\Delta t}</math><br />
 +
Com a derivação é possível calcular a velocidade de um objeto a partir do gráfico <big>s</big>x<big>t</big>, ela fornece a inclinação da reta tangente ao ponto na curva correspondente, sendo essa a velocidade instantânea.
 +
A aceleração é a derivada da velocidade com relação ao tempo:<br />
 +
<math>a=\frac{d \mathbf{v}}{dt}</math>
 +
 
 +
== Unidades de velocidade ==
 +
{| align=right
 +
|[[Ficheiro:velocidadereferencial.png|thumb|Velocidade e referencial. No diagrama acima, a velocidade relativa do objecto em relação a uma câmera sobre trilhos, ao lado da trajetória, movendo-se com a mesma rapidez do objecto, é igual a 0 (pois v<sub>1</sub> = v<sub>2</sub>). A câmera, pois, registrará o objecto "parado" em sua frente.]]
 +
|-
 +
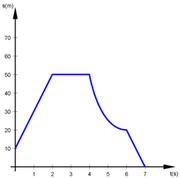
|[[Ficheiro:velocidadegrafico.png|thumb|Gráfico do tempo ''versus'' deslocamento, que permite a inferência da velocidade escalar.]]
 +
|}
 +
 
 +
=== [[Sistema Internacional de Unidades]] (SI) ===
 +
* [[Metro por segundo]] (m/s): unidade de velocidade do [[Sistema Internacional de Unidades|SI]] (1 m/s = 3,6&nbsp;km/h).
 +
 
 +
=== [[Sistema CGS de unidades]] ===
 +
* [[Centímetro]] por segundo (cm/s)
 +
 
 +
=== [[Sistema imperial de medidas]] ===
 +
* Pé por segundo (ft/s)
 +
* [[Milha por hora]] (mph) 
 +
* [[Milha]] por segundo (mps)
 +
 
 +
=== [[Navegação marítima]] e [[Navegação aérea]] ===
 +
* O [[nó (unidade)|nó]] é uma unidade de medida da velocidade, utilizada na navegação marítima e aérea, equivalente a uma [[milha náutica]] por hora.
 +
 
 +
=== [[Aeronáutica]] ===
 +
* [[Número de Mach]]. O Número de Mach (M) é uma medida de [[velocidade relativa]] que se define como o quociente entre a velocidade dum objeto e a [[velocidade do som]] no meio em que se move dito objeto. É um [[número adimensional]] tipicamente usado para descrever a velocidade dos aviões. Mach 1 equivale à velocidade do som; Mach 2 é duas vezes a velocidade do som; e assim sucessivamente. A velocidade do som no ar é de 340 m/s (1224&nbsp;km/h).
 +
 
 +
=== [[Unidades de Planck|Unidades naturais]] ===
 +
* [[Velocidade da luz]] no vácuo = 299&nbsp;792&nbsp;458 m/s (convencionalmente 300&nbsp;000&nbsp;km/s). É a maior velocidade que se pode atingir no Universo segundo a [[Relatividade restrita|Teoria Restrita da Relatividade]] de [[Einstein]].
 +
 
 +
=== Outras unidades ===
 +
* [[Quilômetro por hora]] (km/h)
 +
* Quilômetro por segundo (km/s)
 +
 
 +
=={{Ver também}}==
 +
{{wikcionário}}
 +
*[[Velocidade supersónica]]
 +
*[[Velocidade subsônica]]
 +
*[[Velocidade terminal]]
 +
*[[Velocimetria laser]]
 +
*[[Velocidade angular]]
 +
*[[Velocidade da luz]]
 +
*[[Velocidade de escape]]
 +
*[[Velocidade de reação]]
 +
 
 +
[[Categoria:Tecnologia]]
 +
[[Categoria:Mecânica clássica]]
 +
[[Categoria:Grandezas físicas]]
 +
 
 +
[[af:Snelheid]]
 +
[[als:Geschwindigkeit]]
 +
[[am:ፍጥነት]]
 +
[[an:Velocidat]]
 +
[[ar:سرعة متجهة]]
 +
[[as:বেগ]]
 +
[[be:Хуткасць]]
 +
[[be-x-old:Хуткасьць]]
 +
[[bg:Скорост]]
 +
[[bn:গতিবেগ]]
 +
[[ca:Velocitat]]
 +
[[ckb:خێرایی]]
 +
[[cs:Rychlost]]
 +
[[cy:Cyflymder]]
 +
[[da:Hastighed]]
 +
[[de:Geschwindigkeit]]
 +
[[el:Ταχύτητα]]
 +
[[en:Velocity]]
 +
[[eo:Vektora rapido]]
 +
[[es:Velocidad]]
 +
[[et:Kiirus]]
 +
[[eu:Abiadura]]
 +
[[fa:سرعت برداری]]
 +
[[fi:Nopeus]]
 +
[[fiu-vro:Kibõhusvektor]]
 +
[[fr:Vitesse]]
 +
[[frr:Faard]]
 +
[[fy:Snelheid]]
 +
[[ga:Treoluas]]
 +
[[gl:Velocidade]]
 +
[[he:מהירות]]
 +
[[hi:वेग]]
 +
[[hr:Brzina]]
 +
[[ht:Vitès mwayèn]]
 +
[[hu:Sebesség]]
 +
[[ia:Velocitate]]
 +
[[id:Kecepatan]]
 +
[[io:Veloceso]]
 +
[[is:Hraði]]
 +
[[it:Velocità]]
 +
[[ja:速度]]
 +
[[jv:Kacepetan]]
 +
[[kk:Жылдамдық]]
 +
[[km:ល្បឿន]]
 +
[[ko:속도]]
 +
[[la:Velocitas]]
 +
[[lv:Ātrums]]
 +
[[ml:പ്രവേഗം]]
 +
[[mr:वेग]]
 +
[[ms:Halaju]]
 +
[[my:အလျင်]]
 +
[[nl:Snelheid]]
 +
[[nn:Hastigheit]]
 +
[[no:Hastighet]]
 +
[[oc:Velocitat]]
 +
[[pl:Prędkość]]
 +
[[pms:Andi]]
 +
[[pnb:ولاسٹی]]
 +
[[qu:Utqa kay]]
 +
[[ro:Viteză]]
 +
[[ru:Скорость]]
 +
[[rue:Швыдкость]]
 +
[[sh:Brzina]]
 +
[[simple:Velocity]]
 +
[[sk:Rýchlosť (fyzikálna veličina)]]
 +
[[sl:Hitrost]]
 +
[[sq:Shpejtësia]]
 +
[[sr:Брзина]]
 +
[[sv:Hastighet]]
 +
[[ta:திசைவேகம்]]
 +
[[tg:Суръат]]
 +
[[th:ความเร็ว]]
 +
[[tl:Belosidad]]
 +
[[tr:Hız]]
 +
[[uk:Швидкість]]
 +
[[ur:سمتار]]
 +
[[uz:Tezlik]]
 +
[[vi:Vận tốc]]
 +
[[war:Velosidad]]
 +
[[yi:גיכקייט]]
 +
[[zh:速度]]
 +
[[zh-min-nan:Sok-tō͘]]

Edição das 21h39min de 1 de setembro de 2012

Predefinição:Sem-fontes Predefinição:Mecânica Clássica Na física, velocidade relaciona a variação da posição no espaço em relação ao tempo, ou seja, qual a distância percorrida por um corpo num determinado intervalo temporal. É uma grandeza vetorial, possuindo direção, sentido e módulo, esse último chamado de rapidez e de dimensões [L][T]-1, sendo medida no SI em metros por segundo (m/s ou ms-1). Em geral, os símbolos da velocidade são v ou 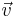\vec{v}, o primeiro para a velocidade escalar e o segundo para o vetor velocidade. A variação da velocidade em relação ao tempo é a aceleração.

Conteúdo

 [ocultar] 

Equações de velocidade

Velocidade é um conceito fundamental para a mecânica clássica. Foi a partir desse que os primeiros físicos puderam desenvolver o estudo do movimento dos corpos, tornando-se capazes de descrever trajetórias através de funções matemáticas. Isaac Newton, pai da mecânica clássica, desenvolveu o cálculo diferencial a partir desse estudo. Há dois tipos de movimentos considerados mais simples: o movimento retilíneo uniforme(MRU) e o movimento retílineo uniformemente variado(MRUV), que são representados por equações lineares e quadrádicas respectivamente. Para outros tipos de movimento mais complexos utiliza-se a derivada.

Movimento Retílineo Uniforme

É o movimento descrito por objetos com velocidade constante, para tal, é preciso que a resultante das forças que atuam sobre o corpo seja nula. Dado um deslocamento \Delta s, em um tempo \Delta t A velocidade escalar v é dada por:
\mathbf{v}=\frac{\Delta s}{\Delta t}.
Somente no MRU a velocidade de um corpo a qualquer instante é igual à sua velocidade média. A equação do espaço S em função do tempo t, a partir de um ponto S_o é:
S=S_o+\mathbf{v}t

O gráfico sxt desse movimento é uma linha reta cuja tangente do ângulo de inclinação dessa reta, em relação ao eixo t é o valor da velocidade.

Movimento Retilíneo Uniformemente Variado

É o movimento de objetos que variam sua velocidade de forma constante, ou seja, possuem aceleração constante. No MRUV a equação da aceleração é análoga à da velocidade no MRU; e a equação de velocidade no MRUV é análoga à do espaço no MRU.
a=\frac{\Delta \mathbf{v}}{\Delta t}

\mathbf{v}=\mathbf{v}_o+at
E a equação do espaço é a seguinte:
S=S_o+\mathbf{v}_ot+\frac{at^2}{2}
O gráfico sxt desse movimento é uma parábola.

Veja mais em movimento retilíneo.

Derivada

Os dois movimentos acima só ocorrem em condições muito especificas, para estudar os movimentos dos corpos como ocorrem na natureza Newton desenvolveu a derivada, para calcular a velocidade instantânea de um corpo em certo instante é necessário usar limite, medindo-se uma variação infinitesimal de espaço em um intervalo infinitesimal de tempo.
\mathbf{v}=\lim_{\Delta t \rightarrow 0}\frac{\Delta s}{\Delta t}=\frac{ds}{dt}
Da definição de derivada:
\mathbf{v}=\frac{ds}{dt}=\lim_{\Delta t \rightarrow 0}\frac{S\left(t+\Delta t\right)-S(t)}{\Delta t}
Com a derivação é possível calcular a velocidade de um objeto a partir do gráfico sxt, ela fornece a inclinação da reta tangente ao ponto na curva correspondente, sendo essa a velocidade instantânea. A aceleração é a derivada da velocidade com relação ao tempo:
a=\frac{d \mathbf{v}}{dt}

Unidades de velocidade

Velocidade e referencial. No diagrama acima, a velocidade relativa do objecto em relação a uma câmera sobre trilhos, ao lado da trajetória, movendo-se com a mesma rapidez do objecto, é igual a 0 (pois v1 = v2). A câmera, pois, registrará o objecto "parado" em sua frente.
Gráfico do tempo versus deslocamento, que permite a inferência da velocidade escalar.

Sistema Internacional de Unidades (SI)

Sistema CGS de unidades

Sistema imperial de medidas

Navegação marítima e Navegação aérea

  • O nó é uma unidade de medida da velocidade, utilizada na navegação marítima e aérea, equivalente a uma milha náutica por hora.

Aeronáutica

  • Número de Mach. O Número de Mach (M) é uma medida de velocidade relativa que se define como o quociente entre a velocidade dum objeto e a velocidade do som no meio em que se move dito objeto. É um número adimensional tipicamente usado para descrever a velocidade dos aviões. Mach 1 equivale à velocidade do som; Mach 2 é duas vezes a velocidade do som; e assim sucessivamente. A velocidade do som no ar é de 340 m/s (1224 km/h).

Unidades naturais

Outras unidades

Predefinição:Ver também

Predefinição:Wikcionário

pnb:ولاسٹیrue:Швыдкостьwar:Velosidad

Disponível em "http://wiki.stoa.usp.br/index.php?title=Teced/textos/Grupo_3&oldid=15344"
Ferramentas pessoais
Espaços nominais

Variantes
Ações
Navegação
Imprimir/exportar
Ferramentas
Em outros idiomas