Mudanças entre as edições de "Teced/textos/Grupo 3"
(→Movimento Retilíneo Uniformemente Variado) |
(→Movimento Retilíneo Uniforme) |
||
| (25 edições intermediárias de um usuário não apresentadas) | |||
| Linha 24: | Linha 24: | ||
=== Movimento Retilíneo Uniforme === | === Movimento Retilíneo Uniforme === | ||
| − | É o movimento descrito por objetos com velocidade constante, para tal, é preciso que a resultante das forças que atuam sobre o corpo seja | + | É o movimento descrito por objetos com velocidade constante, para tal, é preciso que a resultante das forças que atuam sobre o corpo seja nula(aceleração nula). Dado um deslocamento <math>\Delta s</math>, em um tempo <math>\Delta t</math> a velocidade escalar '''v''' é dada por:<br /> |
| Linha 39: | Linha 39: | ||
O gráfico <big>s</big>x<big>t</big> desse movimento é uma linha reta cuja tangente do ângulo de inclinação dessa reta, em relação ao eixo '''t''' é o valor da velocidade. | O gráfico <big>s</big>x<big>t</big> desse movimento é uma linha reta cuja tangente do ângulo de inclinação dessa reta, em relação ao eixo '''t''' é o valor da velocidade. | ||
| − | |||
=== Movimento Retilíneo Uniformemente Variado === | === Movimento Retilíneo Uniformemente Variado === | ||
| − | Neste movimento a aceleração | + | Neste movimento a [http://pt.wikipedia.org/wiki/Acelera%C3%A7%C3%A3o aceleração] não é nula. Ou seja, a velocidade varia em função do tempo. Esta variação é linear. Isto é, para um mesmo intervalo de tempo, teremos a mesma variação de velocidade (aceleração constante e diferente de zero). |
No MRUV a equação da aceleração é análoga à da velocidade no MRU; e a equação de velocidade no MRUV é análoga à do espaço no MRU.<br /> | No MRUV a equação da aceleração é análoga à da velocidade no MRU; e a equação de velocidade no MRUV é análoga à do espaço no MRU.<br /> | ||
| + | |||
<math>a=\frac{\Delta \mathbf{v}}{\Delta t}</math><br /> | <math>a=\frac{\Delta \mathbf{v}}{\Delta t}</math><br /> | ||
| + | |||
<math>\mathbf{v}=\mathbf{v}_o+at</math><br /> | <math>\mathbf{v}=\mathbf{v}_o+at</math><br /> | ||
| + | |||
E a equação do espaço é a seguinte:<br /> | E a equação do espaço é a seguinte:<br /> | ||
| + | |||
<math>S=S_o+\mathbf{v}_ot+\frac{at^2}{2}</math><br /> | <math>S=S_o+\mathbf{v}_ot+\frac{at^2}{2}</math><br /> | ||
| + | |||
O gráfico <big>s</big>x<big>t</big> desse movimento é uma parábola. | O gráfico <big>s</big>x<big>t</big> desse movimento é uma parábola. | ||
| + | |||
Veja mais em [http://pt.wikipedia.org/wiki/Movimento_retil%C3%ADneo movimento retilíneo]. | Veja mais em [http://pt.wikipedia.org/wiki/Movimento_retil%C3%ADneo movimento retilíneo]. | ||
| + | |||
=== [http://pt.wikipedia.org/wiki/Derivada Derivada] === | === [http://pt.wikipedia.org/wiki/Derivada Derivada] === | ||
| − | Os dois movimentos | + | Os dois movimentos supracitados só ocorrem em condições muito especificas, para estudar os movimentos dos corpos como ocorrem na natureza Newton desenvolveu a derivada (taxa de variação). Com ela, podemos determinar a velocidade instântanea de um corpo. Para tanto, é necessário usar o conceito de [http://pt.wikipedia.org/wiki/Limite limite], medindo-se uma variação infinitesimal de espaço em um intervalo infinitesimal de tempo.<br /> |
| + | |||
| + | |||
<math>\mathbf{v}=\lim_{\Delta t \rightarrow 0}\frac{\Delta s}{\Delta t}=\frac{ds}{dt}</math><br /> | <math>\mathbf{v}=\lim_{\Delta t \rightarrow 0}\frac{\Delta s}{\Delta t}=\frac{ds}{dt}</math><br /> | ||
| + | |||
| + | |||
Da definição de derivada:<br /> | Da definição de derivada:<br /> | ||
| + | |||
| + | |||
<math>\mathbf{v}=\frac{ds}{dt}=\lim_{\Delta t \rightarrow 0}\frac{S\left(t+\Delta t\right)-S(t)}{\Delta t}</math><br /> | <math>\mathbf{v}=\frac{ds}{dt}=\lim_{\Delta t \rightarrow 0}\frac{S\left(t+\Delta t\right)-S(t)}{\Delta t}</math><br /> | ||
| + | |||
| + | |||
Com a derivação é possível calcular a velocidade de um objeto a partir do gráfico <big>s</big>x<big>t</big>, ela fornece a inclinação da reta tangente ao ponto na curva correspondente, sendo essa a velocidade instantânea. | Com a derivação é possível calcular a velocidade de um objeto a partir do gráfico <big>s</big>x<big>t</big>, ela fornece a inclinação da reta tangente ao ponto na curva correspondente, sendo essa a velocidade instantânea. | ||
A aceleração é a derivada da velocidade com relação ao tempo:<br /> | A aceleração é a derivada da velocidade com relação ao tempo:<br /> | ||
| + | |||
| + | |||
<math>a=\frac{d \mathbf{v}}{dt}</math> | <math>a=\frac{d \mathbf{v}}{dt}</math> | ||
| Linha 71: | Linha 87: | ||
=== Velocidade Limite da Luz === | === Velocidade Limite da Luz === | ||
Atualmente, o maior valor de velocidade que conhecemos é o da velocidade da luz, este sendo igual a <math>3 . 10^8 m/s</math>. Os cientistas acreditam que esse é o valor limite para a velocidade, não podendo ser superado, pois isso causaria uma inversão na ordem dos acontecimentos em relação a seus tempos de ocorrência e causaria uma mudança nas suas relações de causas e efeitos. | Atualmente, o maior valor de velocidade que conhecemos é o da velocidade da luz, este sendo igual a <math>3 . 10^8 m/s</math>. Os cientistas acreditam que esse é o valor limite para a velocidade, não podendo ser superado, pois isso causaria uma inversão na ordem dos acontecimentos em relação a seus tempos de ocorrência e causaria uma mudança nas suas relações de causas e efeitos. | ||
| + | |||
== Unidades de velocidade == | == Unidades de velocidade == | ||
| Linha 78: | Linha 95: | ||
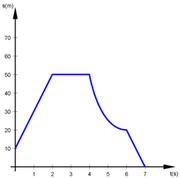
|[[Ficheiro:velocidadegrafico.png|thumb|Gráfico do tempo ''versus'' deslocamento, que permite a inferência da velocidade escalar.]] | |[[Ficheiro:velocidadegrafico.png|thumb|Gráfico do tempo ''versus'' deslocamento, que permite a inferência da velocidade escalar.]] | ||
|} | |} | ||
| + | |||
=== [http://pt.wikipedia.org/wiki/Sistema_Internacional_de_Unidades Sistema Internacional de Unidades] (SI) === | === [http://pt.wikipedia.org/wiki/Sistema_Internacional_de_Unidades Sistema Internacional de Unidades] (SI) === | ||
* [http://en.wikipedia.org/wiki/Metre_per_second Metro por segundo] (m/s): unidade de velocidade do [http://nl.wikipedia.org/wiki/SI-stelsel SI] (1 m/s = 3,6 km/h). | * [http://en.wikipedia.org/wiki/Metre_per_second Metro por segundo] (m/s): unidade de velocidade do [http://nl.wikipedia.org/wiki/SI-stelsel SI] (1 m/s = 3,6 km/h). | ||
| + | |||
=== Conversão entre km/h e m/s === | === Conversão entre km/h e m/s === | ||
| Linha 91: | Linha 110: | ||
<math>\frac{km}{h}</math> ÷ <math> 3,6 = \frac{m}{s}</math> | <math>\frac{km}{h}</math> ÷ <math> 3,6 = \frac{m}{s}</math> | ||
| + | |||
=== [http://pt.wikipedia.org/wiki/Sistema_CGS_de_unidades Sistema CGS de unidades] === | === [http://pt.wikipedia.org/wiki/Sistema_CGS_de_unidades Sistema CGS de unidades] === | ||
* [http://pt.wikipedia.org/wiki/Cent%C3%ADmetro Centímetro] por segundo (cm/s) | * [http://pt.wikipedia.org/wiki/Cent%C3%ADmetro Centímetro] por segundo (cm/s) | ||
| + | |||
=== [http://pt.wikipedia.org/wiki/Sistema_imperial_de_medidas Sistema imperial de medidas] === | === [http://pt.wikipedia.org/wiki/Sistema_imperial_de_medidas Sistema imperial de medidas] === | ||
| Linha 99: | Linha 120: | ||
* [http://pt.wikipedia.org/wiki/Milha_por_hora Milha por hora] (mph) | * [http://pt.wikipedia.org/wiki/Milha_por_hora Milha por hora] (mph) | ||
* [http://pt.wikipedia.org/wiki/Milha Milha] por segundo (mps) | * [http://pt.wikipedia.org/wiki/Milha Milha] por segundo (mps) | ||
| − | |||
=== [http://pt.wikipedia.org/wiki/Navega%C3%A7%C3%A3o_mar%C3%ADtima Navegação marítima] e [http://pt.wikipedia.org/wiki/Navega%C3%A7%C3%A3o_a%C3%A9rea Navegação aérea] === | === [http://pt.wikipedia.org/wiki/Navega%C3%A7%C3%A3o_mar%C3%ADtima Navegação marítima] e [http://pt.wikipedia.org/wiki/Navega%C3%A7%C3%A3o_a%C3%A9rea Navegação aérea] === | ||
* O [http://pt.wikipedia.org/wiki/N%C3%B3_(unidade) nó] é uma unidade de medida da velocidade, utilizada na navegação marítima e aérea, equivalente a uma [http://pt.wikipedia.org/wiki/Milha_n%C3%A1utica milha náutica] por hora. | * O [http://pt.wikipedia.org/wiki/N%C3%B3_(unidade) nó] é uma unidade de medida da velocidade, utilizada na navegação marítima e aérea, equivalente a uma [http://pt.wikipedia.org/wiki/Milha_n%C3%A1utica milha náutica] por hora. | ||
| + | |||
=== [http://pt.wikipedia.org/wiki/Aeron%C3%A1utica Aeronáutica] === | === [http://pt.wikipedia.org/wiki/Aeron%C3%A1utica Aeronáutica] === | ||
* [http://pt.wikipedia.org/wiki/N%C3%BAmero_de_Mach Número de Mach]. O Número de Mach (M) é uma medida de [http://pt.wikipedia.org/w/index.php?title=Velocidade_relativa&action=edit&redlink=1 velocidade relativa] que se define como o quociente entre a velocidade dum objeto e a [http://pt.wikipedia.org/wiki/Velocidade_do_som velocidade do som] no meio em que se move dito objeto. É um [http://pt.wikipedia.org/wiki/N%C3%BAmero_adimensional número adimensional] tipicamente usado para descrever a velocidade dos aviões. Mach 1 equivale à velocidade do som; Mach 2 é duas vezes a velocidade do som; e assim sucessivamente. A velocidade do som no ar é de 340 m/s (1224 km/h). | * [http://pt.wikipedia.org/wiki/N%C3%BAmero_de_Mach Número de Mach]. O Número de Mach (M) é uma medida de [http://pt.wikipedia.org/w/index.php?title=Velocidade_relativa&action=edit&redlink=1 velocidade relativa] que se define como o quociente entre a velocidade dum objeto e a [http://pt.wikipedia.org/wiki/Velocidade_do_som velocidade do som] no meio em que se move dito objeto. É um [http://pt.wikipedia.org/wiki/N%C3%BAmero_adimensional número adimensional] tipicamente usado para descrever a velocidade dos aviões. Mach 1 equivale à velocidade do som; Mach 2 é duas vezes a velocidade do som; e assim sucessivamente. A velocidade do som no ar é de 340 m/s (1224 km/h). | ||
| + | |||
=== [http://pt.wikipedia.org/wiki/Unidades_de_Planck Unidades naturais] === | === [http://pt.wikipedia.org/wiki/Unidades_de_Planck Unidades naturais] === | ||
* [http://pt.wikipedia.org/wiki/Velocidade_da_luz Velocidade da luz] no vácuo = 299 792 458 m/s (convencionalmente 300 000 km/s). É a maior velocidade que se pode atingir no Universo segundo a [http://pt.wikipedia.org/wiki/Relatividade_restrita Teoria Restrita da Relatividade] de [http://pt.wikipedia.org/wiki/Einstein Einstein]. | * [http://pt.wikipedia.org/wiki/Velocidade_da_luz Velocidade da luz] no vácuo = 299 792 458 m/s (convencionalmente 300 000 km/s). É a maior velocidade que se pode atingir no Universo segundo a [http://pt.wikipedia.org/wiki/Relatividade_restrita Teoria Restrita da Relatividade] de [http://pt.wikipedia.org/wiki/Einstein Einstein]. | ||
| + | |||
=== Outras unidades === | === Outras unidades === | ||
* [http://pt.wikipedia.org/wiki/Quil%C3%B4metro_por_hora Quilômetro por hora] (km/h) | * [http://pt.wikipedia.org/wiki/Quil%C3%B4metro_por_hora Quilômetro por hora] (km/h) | ||
* [http://pt.wikipedia.org/wiki/Quil%C3%B4metro_por_segundo Quilômetro por segundo] (km/s) | * [http://pt.wikipedia.org/wiki/Quil%C3%B4metro_por_segundo Quilômetro por segundo] (km/s) | ||
| + | |||
=='''Ver também'''== | =='''Ver também'''== | ||
Edição atual tal como às 14h10min de 10 de setembro de 2012
Conteúdo[ocultar] |
[editar] Velocidade
Na física, velocidade relaciona a variação da posição no espaço em relação ao tempo, ou seja, velocidade é a distância percorrida por um corpo num determinado intervalo de tempo. É uma grandeza vetorial, possuindo direção, sentido e módulo, esse último chamado de rapidez e de dimensões [L][T]-1, sendo medida no SI em metros por segundo (m/s ou ms-1). Em geral, os símbolos da velocidade são v ou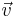 
, o primeiro para a velocidade escalar e o segundo para o vetor velocidade.
A grandeza responsável pela variação da velocidade em relação ao tempo é denominada aceleração.
[editar] Equações de velocidade
Velocidade é um conceito fundamental para a mecânica clássica. Foi a partir deste conceito que foi desenvolvido o estudo do movimento dos corpos, e, consequentemente, a descrição de trajetórias através de funções matemáticas. Isaac Newton, pai da mecânica clássica, desenvolveu o cálculo diferencial a partir desse estudo. Entre os diversos tipos de movimentos existentes, destacam-se os dois mais elementares:
Movimento retilíneo uniforme (MRU) - Representado por equações lineares (primeiro grau).
Exemplo: Qualquer objeto se movimentando com velocidade constante.
Movimento retilíneo uniformemente variado (MRUV) - Representado por equações quadráticas (segundo grau).
Exemplo: Qualquer objetivo se movimentando com velocidade variável em função do tempo.
Para outros tipos de movimento mais complexos utiliza-se o conceito de derivada.
[editar] Movimento Retilíneo Uniforme
É o movimento descrito por objetos com velocidade constante, para tal, é preciso que a resultante das forças que atuam sobre o corpo seja nula(aceleração nula). Dado um deslocamento 
, em um tempo 
a velocidade escalar v é dada por:
.
Uma característica exclusiva do MRU é a de que a velocidade de um corpo em qualquer instante é igual à sua velocidade média.
A equação do espaço S em função do tempo t, a partir de um ponto 
é:
O gráfico sxt desse movimento é uma linha reta cuja tangente do ângulo de inclinação dessa reta, em relação ao eixo t é o valor da velocidade.
[editar] Movimento Retilíneo Uniformemente Variado
Neste movimento a aceleração não é nula. Ou seja, a velocidade varia em função do tempo. Esta variação é linear. Isto é, para um mesmo intervalo de tempo, teremos a mesma variação de velocidade (aceleração constante e diferente de zero).
No MRUV a equação da aceleração é análoga à da velocidade no MRU; e a equação de velocidade no MRUV é análoga à do espaço no MRU.
E a equação do espaço é a seguinte:
O gráfico sxt desse movimento é uma parábola.
Veja mais em movimento retilíneo.
[editar] Derivada
Os dois movimentos supracitados só ocorrem em condições muito especificas, para estudar os movimentos dos corpos como ocorrem na natureza Newton desenvolveu a derivada (taxa de variação). Com ela, podemos determinar a velocidade instântanea de um corpo. Para tanto, é necessário usar o conceito de limite, medindo-se uma variação infinitesimal de espaço em um intervalo infinitesimal de tempo.
Da definição de derivada:
Com a derivação é possível calcular a velocidade de um objeto a partir do gráfico sxt, ela fornece a inclinação da reta tangente ao ponto na curva correspondente, sendo essa a velocidade instantânea.
A aceleração é a derivada da velocidade com relação ao tempo:
[editar] Velocidade Limite da Luz
Atualmente, o maior valor de velocidade que conhecemos é o da velocidade da luz, este sendo igual a 
. Os cientistas acreditam que esse é o valor limite para a velocidade, não podendo ser superado, pois isso causaria uma inversão na ordem dos acontecimentos em relação a seus tempos de ocorrência e causaria uma mudança nas suas relações de causas e efeitos.
[editar] Unidades de velocidade
 |
 |
[editar] Sistema Internacional de Unidades (SI)
- Metro por segundo (m/s): unidade de velocidade do SI (1 m/s = 3,6 km/h).
[editar] Conversão entre km/h e m/s
Como vimos anteriormente, a unidade padrão de velocidade é o m/s. Mas o que utilizamos no nosso dia-a-dia é a unidade km/h, por isso, é importante saber efetuar a conversão entre o km/h e o m/s, que é dada pela seguinte relação:
× 
e
÷ 
[editar] Sistema CGS de unidades
- Centímetro por segundo (cm/s)
[editar] Sistema imperial de medidas
- Pé por segundo (ft/s)
- Milha por hora (mph)
- Milha por segundo (mps)
[editar]
- O nó é uma unidade de medida da velocidade, utilizada na navegação marítima e aérea, equivalente a uma milha náutica por hora.
[editar] Aeronáutica
- Número de Mach. O Número de Mach (M) é uma medida de velocidade relativa que se define como o quociente entre a velocidade dum objeto e a velocidade do som no meio em que se move dito objeto. É um número adimensional tipicamente usado para descrever a velocidade dos aviões. Mach 1 equivale à velocidade do som; Mach 2 é duas vezes a velocidade do som; e assim sucessivamente. A velocidade do som no ar é de 340 m/s (1224 km/h).
[editar] Unidades naturais
- Velocidade da luz no vácuo = 299 792 458 m/s (convencionalmente 300 000 km/s). É a maior velocidade que se pode atingir no Universo segundo a Teoria Restrita da Relatividade de Einstein.
[editar] Outras unidades
- Quilômetro por hora (km/h)
- Quilômetro por segundo (km/s)
