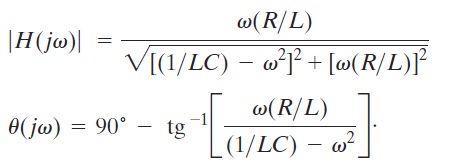Mudanças entre as edições de "CircuitoRLC"
| (Uma edição intermediária de um usuário não apresentada) | |||
| Linha 1: | Linha 1: | ||
| − | + | __TOC__ | |
== Introdução == | == Introdução == | ||
Um circuito RLC série é composto por uma fonte de tensão (alternada ou contínua), um resistor, um capacitor e um indutor ligados em série. | Um circuito RLC série é composto por uma fonte de tensão (alternada ou contínua), um resistor, um capacitor e um indutor ligados em série. | ||
| Linha 17: | Linha 17: | ||
<math>\varepsilon = \frac{Q}{C}+ L\frac{dI}{dt} +RI</math> | <math>\varepsilon = \frac{Q}{C}+ L\frac{dI}{dt} +RI</math> | ||
| − | <math>\varepsilon = \frac{Q}{C}+ L \frac{d^2Q}{dt^2} + R \frac{dQ}{dt}</math> | + | Chegamos finalmente a equação que descreve o comportamento do sistema. |
| + | |||
| + | <math>\varepsilon = \frac{Q}{C}+ L \frac{d^2Q}{dt^2} + R \frac{dQ}{dt}</math> | ||
| + | |||
| + | Para conhecermos o funcionamento deste circuito, precisamos obter soluções <math>Q(t)</math> da equação acima. Este é um problema matemático bem conhecido, cujas características principais discutiremos em seguida. | ||
| + | |||
| + | A equação diferencial é de segunda ordem, pois envolve a derivada segunda da carga <math>Q</math> em relação ao tempo. | ||
O grande diferencial do circuito RLC é visto quando em tensão alternada, já que é possível fazer os chamados "filtros" alterando os valores do capacitor e do indutor. Desta forma é possível obter os chamados filtros "passa-baixa", "passa-alta", entre outros. | O grande diferencial do circuito RLC é visto quando em tensão alternada, já que é possível fazer os chamados "filtros" alterando os valores do capacitor e do indutor. Desta forma é possível obter os chamados filtros "passa-baixa", "passa-alta", entre outros. | ||
Edição atual tal como às 18h27min de 17 de setembro de 2013
Conteúdo[ocultar] |
[editar] Introdução
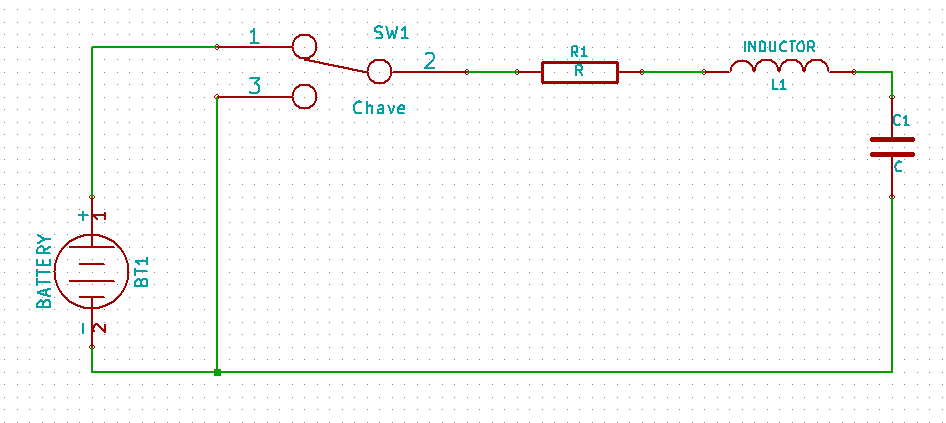
Um circuito RLC série é composto por uma fonte de tensão (alternada ou contínua), um resistor, um capacitor e um indutor ligados em série.
[editar] Analisando em corrente contínua.
No circuito acima temos uma bateria, e um circuito RLC, enquanto o a chave está na posição (1) a expressão que pode definir esse circuito é da forma de:
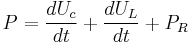
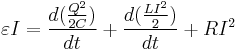
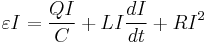
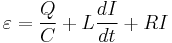
Chegamos finalmente a equação que descreve o comportamento do sistema.
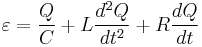
Para conhecermos o funcionamento deste circuito, precisamos obter soluções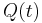 
da equação acima. Este é um problema matemático bem conhecido, cujas características principais discutiremos em seguida.
A equação diferencial é de segunda ordem, pois envolve a derivada segunda da carga 
em relação ao tempo.
O grande diferencial do circuito RLC é visto quando em tensão alternada, já que é possível fazer os chamados "filtros" alterando os valores do capacitor e do indutor. Desta forma é possível obter os chamados filtros "passa-baixa", "passa-alta", entre outros.
Segue abaixo o exemplo do filtro "Passa-faixa"
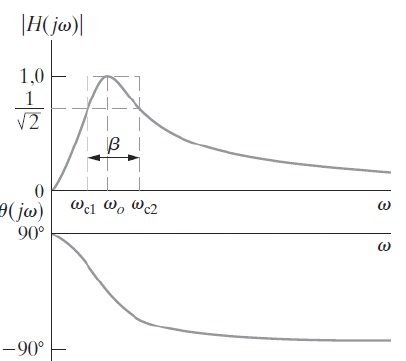
Circuito Passa-Faixa Como o próprio nome diz, o circuito passa-faixa atenua todas as frequências (medidas sobre o resistor R) que não estiverem no range definido na figura abaixo, conforme equação característica a seguir:
Referência: http://www.cpdee.ufmg.br/~danilomelges//circ3/Aula7-CircuitosSeletoresFrequenciaPt2.pdf
