Mudanças entre as edições de "Usuário:Calsaverini/data"

De Stoa
Ir para: navegação, pesquisa
(Criou página com '== Expansão para função de partição em baixas temperaturas == Imagine que se quer calcular <math> \displaystyle Z = \sum_{x} e^{-\beta E(x)}</math> para <math>\beta = \fra…')
 
 
(Uma edição intermediária de um usuário não apresentada)
Linha 1: Linha 1:
 +
= Bobagens que não parecem chegar em lugar algum mas não saem da minha cabeça =
 
== Expansão para função de partição em baixas temperaturas ==
 
== Expansão para função de partição em baixas temperaturas ==
−
Imagine que se quer calcular  
+
Imagine que se quer calcular <math> \displaystyle Z = \sum_{x} e^{-\beta E(x)}</math> para <math>\beta = \frac{1}{T} \to\infty</math>. Escreva como <math> Z = \int e^{-E/T} \rho(E) dE </math>, onde <math> \rho(E) = \sum_{x} \delta(E - E(x))</math>. Note que:
−
<math> \displaystyle Z = \sum_{x} e^{-\beta E(x)}</math>  
+
−
para <math>\beta = \frac{1}{T} \to\infty</math>.  
+
  
−
write it as:
+
<math>\int e^{-\frac{Ax^2}{2}+ B x} dx = \sqrt{\frac{2\pi}{A}}e^{\frac{B^2}{2A}}</math>
  
−
rho(E) = \sum_{x} \delta(E - E(x))
+
Então, se <math>B = i\sqrt{2E}</math> e <math>\displaystyle T = A</math> temos <math> e^{-\frac{E}{T}} = \int du \exp\left[-\frac{T u^2}{2}- i\sqrt{2E} u\right] </math> e então:
  
−
Z = \int exp(-E/T) rho(E) dE
+
<math> Z = \int du\; e^{-\frac{Tu^2}{2}} \int dE \; e^{-i\sqrt{2E} u} \rho(E) </math>
  
 +
vamos chamar <math> \Xi(u) = \int dE e^{-i\sqrt{2E}u} \rho(E)</math> e fazer a mudança de variáveis <math>E = \frac{p^2}{2}</math> então:
 +
<math> \Xi(u) = \int p dp\; e^{-ipu} \rho\left(\frac{p^2}{2}\right)</math>
  
 +
Se me interesso por <math> T \to 0</math>, posso expandir em série de potências:
  
−
note that: \int exp(-1/2 A x² + B x) dx = sqrt(2\pi/A) exp(1/2 B² / A)
+
<math> Z = \int du\; e^{-\frac{T u^2}{2}} \Xi(u) </math>
  
−
So, if E = -B²/2 (B = i\sqrt{2E} ) and T = A we have
+
<math> = \int du\;\Xi(u) \sum_{n=0}^{\infty} \frac{(-1)^n T^n u^{2n}}{n!}</math>
 +
<math> = \sum_{n=0}^{\infty} \frac{(-1)^n T^n}{n!} \int du\;\Xi(u) u^{2n}</math>
  
−
exp(-E/T) = \int du exp(-1/2 T u² - i\sqrt{2E} u)  
+
<math> = \int du \;\Xi(u)- \frac{1}{2} T \int du \;\Xi(u) u^2 + \ldots</math>
  
−
and then:
 
  
 +
Mas <math> \Xi(u)</math> está na forma de uma transformada de Fourier, <math> \Xi(u) = \int dp\; e^{-ipu} F(p)</math>, com <math>F(p) = p \rho\left(\frac{p^2}{2}\right)</math>
  
−
Z = \int du exp(-1/2 T u²) \int dE exp(-i\sqrt{2E} u) \rho(E)
+
E então podemos escrever:
  
−
call Chi(u) = \int dE exp(-i\sqrt{2E}u) \rho(E)  
+
<math>\int du\;\Xi(u) u^{2n} = \int du\,dp\; F(p) e^{-ipu} u^{2n}</math>
 +
<math> = \int dp F(p)(-i\partial_p)^{2n}\delta(p) = (-1)^n F^{2n}(0)</math>
  
−
and make a change of variables
+
E então:
−
p = \sqrt{2E}
+
−
E = p²/2  dE = p dp
+
  
−
then:
+
<math>Z =  \sum_{n=0}^{\infty} \frac{ F_{n}}{n!} T^n </math>
  
−
Chi(u) = \int dp exp(-ipu) p\rho(p²/2)  
+
onde <math> \displaystyle F_{n} = \lim_{p\to 0} \frac{d^{2n}}{dp^{2n}} \left[p \rho\left(\frac{p^2}{2}\right)\right]</math>
  
−
and call
+
lembrando a definição de <math> \rho(E)</math>:
  
−
\Rho(p) = p\rho(p²/2)  = p \sum_{x} \delta(p²/2 - E(x))
+
<math> \displaystyle F_{n} = \lim_{p\to 0} \frac{d^{2n}}{dp^{2n}} \left[p \sum_{x} \delta\left(\frac{p^2}{2} - E(x)\right)\right]</math>
  
−
If I'm interested in T -> 0 then I can expand Z in powers of T:
+
parece não chegar em lugar algum porque calcular <math> \rho(E)</math> é tão difícil quando a própria função de partição, então blerghs...
−
 
+
−
Z = \int du exp(-1/2 T u²) \tilde{\Rho}(u)
+
−
 
+
−
= \int du \tilde{\Rho}(u) \left(1 - 1/2 T u² + ...\right)
+
−
 
+
−
= \int du \tilde{\Rho}(u) - 1/2 T u² \int du \tilde{\Rho}(u) u²
+
−
 
+
−
 
+
−
\tilde{\Rho}(u)  = \int dp exp(-ipu) \Rho(p)
+
−
 
+
−
\int du \tilde{\Rho}(u) = \Rho(0) = lim_{p->0} p \sum{x} \delta(p²/2 - E(x))
+
−
\int du u² \tilde{\Rho}(u) = \Rho''(0)
+
−
 
+
−
 
+
−
Z = \Rho(0) - T/2 \Rho''(0) + O(T²)
+

Edição atual tal como às 16h40min de 12 de setembro de 2010

[editar] Bobagens que não parecem chegar em lugar algum mas não saem da minha cabeça

[editar] Expansão para função de partição em baixas temperaturas

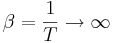Imagine que se quer calcular \displaystyle Z = \sum_{x} e^{-\beta E(x)} para \beta = \frac{1}{T} \to\infty. Escreva como 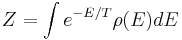Z = \int e^{-E/T} \rho(E) dE , onde 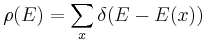\rho(E) = \sum_{x} \delta(E - E(x)). Note que:

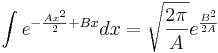
\int e^{-\frac{Ax^2}{2}+ B x} dx = \sqrt{\frac{2\pi}{A}}e^{\frac{B^2}{2A}}

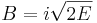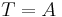Então, se B = i\sqrt{2E} e \displaystyle T = A temos e^{-\frac{E}{T}} = \int du \exp\left[-\frac{T u^2}{2}- i\sqrt{2E} u\right] e então:

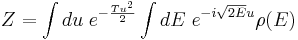
Z = \int du\; e^{-\frac{Tu^2}{2}} \int dE \; e^{-i\sqrt{2E} u} \rho(E)

vamos chamar \Xi(u) = \int dE e^{-i\sqrt{2E}u} \rho(E) e fazer a mudança de variáveis E = \frac{p^2}{2} então: \Xi(u) = \int p dp\; e^{-ipu} \rho\left(\frac{p^2}{2}\right)

Se me interesso por T \to 0, posso expandir em série de potências:

Z = \int du\; e^{-\frac{T u^2}{2}} \Xi(u)

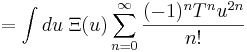
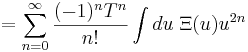
= \int du\;\Xi(u) \sum_{n=0}^{\infty} \frac{(-1)^n T^n u^{2n}}{n!} = \sum_{n=0}^{\infty} \frac{(-1)^n T^n}{n!} \int du\;\Xi(u) u^{2n}

= \int du \;\Xi(u)- \frac{1}{2} T \int du \;\Xi(u) u^2 + \ldots


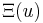Mas \Xi(u) está na forma de uma transformada de Fourier, 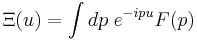\Xi(u) = \int dp\; e^{-ipu} F(p), com F(p) = p \rho\left(\frac{p^2}{2}\right)

E então podemos escrever:

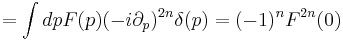
\int du\;\Xi(u) u^{2n} = \int du\,dp\; F(p) e^{-ipu} u^{2n} = \int dp F(p)(-i\partial_p)^{2n}\delta(p) = (-1)^n F^{2n}(0)

E então:

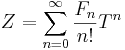
Z = \sum_{n=0}^{\infty} \frac{ F_{n}}{n!} T^n

onde \displaystyle F_{n} = \lim_{p\to 0} \frac{d^{2n}}{dp^{2n}} \left[p \rho\left(\frac{p^2}{2}\right)\right]

lembrando a definição de \rho(E):

\displaystyle F_{n} = \lim_{p\to 0} \frac{d^{2n}}{dp^{2n}} \left[p \sum_{x} \delta\left(\frac{p^2}{2} - E(x)\right)\right]

parece não chegar em lugar algum porque calcular \rho(E) é tão difícil quando a própria função de partição, então blerghs...

Disponível em "http://wiki.stoa.usp.br/index.php?title=Usuário:Calsaverini/data&oldid=12686"
Ferramentas pessoais

Variantes
Ações
Navegação
Imprimir/exportar
Ferramentas