Mudanças entre as edições de "Fap0459/textos/grupo Felipe/Igino/Josiane/Raphael"
(Criou página com '== Introdução == Este trabalho aborda uma apresentação de uma possível abordagem em sala de aula de Física no Ensino Médio sobre o assunto de '''''alavancas''''', usando …') |
(→Atividade) |
||
| (285 edições intermediárias de 5 usuários não apresentadas) | |||
| Linha 1: | Linha 1: | ||
== Introdução == | == Introdução == | ||
| − | Este trabalho | + | Este trabalho tem como objetivo dar fundamentos de [[:pt:Alavancas|alavancas]] a alunos do Ensino Médio usando experiências, simulações, ''experimentos pensados'' e textos. Procuramos dar um enfoque em situações cotidianas do dia-a-dia como uma forma de introduzir ao aluno o conceito de torque sem que este estivesse fora do contexto de sua vivência atual. O proposta se constitui na reprodução do trabalho final da discipina ''FGE0461 - Tecnologia de Ensino de Física I'', produzido pela aluna '''''Josiane Vieira Martins''''', que também é uma das contribuidoras na elaboração deste artigo. |
| − | + | == Sobre a proposta == | |
| − | + | Aquí não é necessário o papel do professor, espera-se que: após o aluno que atenda os pré-requisitos fizer todas as atividades na ordem que aparece ele saiba explicar os ítens expressos no tópico 6. Nos tópicos 8, 9 e 10 colocamos respectivamente exercícios conceituais, atividade e problemas junto com as respostas esperadas para que o aluno possa testar seus conhecimentos. | |
| − | + | == Especificação da População Alvo == | |
| − | * Alunos do Ensino Médio | + | :* Alunos do Ensino Médio |
| − | * Alunos cursando o final do 2º semestre do 1º ano | + | :* Alunos cursando o final do 2º semestre do 1º ano |
| − | + | == Pré-Requisitos == | |
| − | * [[:pt:Funções|Funções]] | + | :* [[:pt:Funções|Funções]] |
| − | * [[:pt:Equações do 1º Grau|Equações do 1º Grau]] | + | :* [[:pt:Equações do 1º Grau|Equações do 1º Grau]] |
| − | * [[:pt:Geometria Plana|Geometria Plana]] | + | :* [[:pt:Geometria Plana|Geometria Plana]] |
| − | * [[:pt:Leis de Newton|Leis de Newton]] | + | :* [[:pt:Vetor (espacial)|Vetores]] |
| − | * [[:pt:Energia|Energia]] | + | :* [[:pt:Leis de Newton|Leis de Newton]] |
| − | * [[:pt:Trabalho|Trabalho]] | + | :* [[:pt:Energia|Energia]] |
| − | * [[:pt:Torque|Torque]] | + | :* [[:pt:Trabalho|Trabalho]] |
| − | * [[:pt:Força de atrito|Força de atrito]] | + | :* [[:pt:Torque|Torque]] |
| − | * [[:pt:Centro de gravidade|Centro de gravidade]] | + | :* [[:pt:Força de atrito|Força de atrito]] |
| + | :* [[:pt:Centro de gravidade|Centro de gravidade]] | ||
| − | + | == Seleção dos Conteúdos que serão abordados == | |
| − | * Máquinas Simples | + | :* Máquinas Simples |
| − | * Alavanca | + | :* Alavanca |
| − | == | + | == Ao final das atividades espera-se que o aluno saiba: == |
| − | # Explicar como uma máquina é capaz de multiplicar a força aplicada sobre ela. | + | :# Explicar como uma máquina é capaz de multiplicar a força aplicada sobre ela. |
| − | # Explicar o que acontece com a distância ao longo do qual atua uma força em uma alavanca. | + | :# Explicar o que acontece com a distância ao longo do qual atua uma força em uma alavanca. |
| − | # Explicar o que acontece com a energia e o trabalho fornecidos em uma alavanca. | + | :# Explicar o que acontece com a energia e o trabalho fornecidos em uma alavanca. |
| − | # Descrever o funcionamento e dar exemplos de alavancas. | + | :# Descrever o funcionamento e dar exemplos de alavancas. |
| − | # Diferenciar os tipos de alavancas. | + | :# Diferenciar os tipos de alavancas. |
| − | # Resolver problemas que envolvam alavancas. | + | :# Resolver problemas que envolvam alavancas. |
| + | |||
| + | == Seqüência de Aprendizagem == | ||
| + | |||
| + | ==== Texto 1 ==== | ||
| + | <center> | ||
| + | {| border="0" cellpadding="0" cellspacing="15" | ||
| + | |- | ||
| + | ! | ||
| + | [[Arquivo:Figura1.JPG|frame|left|'''Figura 1''']] | ||
| + | |||
| + | ! | ||
| + | {| border="3" cellpadding="15" cellspacing="5" | ||
| + | |- | ||
| + | !Dê-me um lugar para me firmar<br>e um ponto de apoio para minha<br>alavanca que eu deslocarei a Terra.<br> (Arquimedes, cientista grego) | ||
| + | |} | ||
| + | |} | ||
| + | </center> | ||
| + | |||
| + | |||
| + | |||
| + | Este texto vai permitir que ao final dele você possa estar entendendo a citação de Arquimedes e o que acontece na figura 1. Com a evolução, o homem criou instrumentos para facilitar as suas atividades de coleta, pesca e caça que facilitavam ou ampliava sua força, esses instrumentos são chamados de máquinas simples. Dentre as máquinas simples a mais comum é alavanca. Uma alavanca é uma barra que pode girar em torno de um ponto de apoio, temos que a alavanca é constituída de: ponto de apoio, força potente, força resistente, braço da força potente e braço da força resistente. Sendo que o braço da força potente é a distância do ponto que esta sendo aplicado a força potente ao ponto de apoio e o braço da força resistente é a distancia que esta sendo aplicada a força resistente ao ponto de apoio.<br> | ||
| + | |||
| + | [[Arquivo:Figura2.JPG|frame|center|'''Figura 2''']] | ||
| + | |||
| + | Sem as alavancas seria muito difícil fazer atividades como trocar o pneu do carro e tirar um parafuso. | ||
| + | |||
| + | ==== Atividade 1 ==== | ||
| + | |||
| + | Verifique experimentalmente em que situação é necessário o uso de mais força: | ||
| + | |||
| + | :* Abrir uma porta aplicando a força o mais próximo possível do eixo da maçaneta e depois o mais <br>longe possível. | ||
| + | :* Girar uma porca usando a mão e usando uma chave de boca. | ||
| + | |||
| + | Percebemos que temos que aplicar mais força quando: abrimos uma porta colocando a força mais próxima do eixo da maçaneta e giramos uma porca usando a mão, esses fatos tornam as propriedades de uma alavanca evidente, no qual as alavancas podem: | ||
| + | |||
| + | :* Alterar a direção de uma força | ||
| + | :* Aplicar uma força a distância | ||
| + | :* Aumentar uma força | ||
| + | :* Aumentar um movimento | ||
| + | |||
| + | ==== Atividade 2 ==== | ||
| + | |||
| + | Utilizando o programa de simulação ''Princípio da Alavanca'' que está no seguinte endereço:<br/> http://pion.sbfisica.org.br/pdc/index.php/por/content/view/full/447/(offset)/20<br/>reproduza as situações abaixo e coloque os resultados na tabela1 e comente os resultados: | ||
| + | |||
| + | :# força resistente = 2x força potente <br/>braço resistente = braço potente | ||
| + | :# força resistente = 2x força potente<br/>braço potente = 2x braço resistente | ||
| + | :# força resistente = 2x força potente<br/>braço resistente = 2x braço potente | ||
| + | |||
| + | |||
| + | |||
| + | <br> | ||
| + | <center> | ||
| + | {| border="2" cellpadding="2" cellspacing="2" | ||
| + | ! | ||
| + | !Força resistente x Braço Resistente | ||
| + | !Força Potente x Braço Potente | ||
| + | |- | ||
| + | !Situação 1 | ||
| + | !_______________________________ | ||
| + | !___________________________ | ||
| + | |- | ||
| + | !Situação 2 | ||
| + | !_______________________________ | ||
| + | !___________________________ | ||
| + | |- | ||
| + | !Situação 3 | ||
| + | !_______________________________ | ||
| + | !___________________________ | ||
| + | |} | ||
| + | '''Tabela 1''' | ||
| + | </center> | ||
| + | <br> | ||
| + | |||
| + | Na simulação foi verificada que na situação 2, um peso menor consegue equilibrar um maior e pela tabela 1 podemos ver que os resultados dos produtos são iguais. Já nas situações 1 e 3 o produto do peso menor com seu braço é sempre menor que o produto do peso maior e seu braço, em que foi observado que o peso maior levanta o menor como também desequilibra a alavanca para seu lado. | ||
| + | |||
| + | Na simulação vimos que para levantar um peso maior utilizando um peso menor alteramos a distância entre a força e o ponto de apoio (situação 2), assim podemos dizer que o efeito de uma alavanca depende da força aplicada e do braço da força, esse efeito é chamado de momento de uma força, que é o produto das forcas pelos braços que foram colocados na Tabela 1. Podemos observar pela tabela 1 que na situação 2 onde houve equilíbrio os momentos são iguais, isso acontece porque quando uma alavanca está no equilíbrio o torque de um lado da alavanca é igual ao outro. | ||
| + | |||
| + | ==== Texto 2 ==== | ||
| + | |||
| + | Temos que para sabermos a vantagem de uma alavanca usamos a seguinte relação: | ||
| + | |||
| + | <center> | ||
| + | <math>vantagem\;\;mec.= \frac{Fr}{Fp}=\frac{Bp}{Br}</math> | ||
| + | <br>'''Equação 1'''</center> | ||
| + | Onde: '''Fr''' = força resistente; '''Fp''' = força potente; '''Br''' = braço resistente; '''Bp''' = braço potente.<br> | ||
| + | As alavancas são classificadas como interfixas, inter-resistentes e interpotente. | ||
| + | |||
| + | |||
| + | =====Alavanca interfixa===== | ||
| + | |||
| + | |||
| + | |||
| + | [[Arquivo:Figura 3.JPG|thumb|left|'''Figura 3''']] | ||
| + | |||
| + | |||
| + | Nesse tipo de alavanca o ponto de apoio está entre os pontos onde são aplicados as forças potentes e forças resistentes como é mostrado na Figura.<br>[[Arquivo:Figura 4.JPG|thumb|left|'''Figura 4''']] | ||
| + | |||
| + | |||
| + | Como exemplo de alavanca interfixa temos a tesoura, que é uma associação de alavancas interfixas que é mostrada na Figura. <br> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | =====Alavanca Inter-Resistente===== | ||
| + | |||
| + | |||
| + | |||
| + | [[Arquivo:Figura 5.JPG|thumb|left|'''Figura 5''']] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
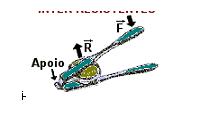
| + | Nesse tipo de alavanca a força resistente está entre o ponto de apoio e a força potente.<br>[[Arquivo:Figura 6.JPG|thumb|left|'''Figura 6''']] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | O martelo é um exemplo de alavanca inter-resistente.<br> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | =====Alavanca Interpotente===== | ||
| + | |||
| + | |||
| + | Temos que a força potente está entre o ponto de apoio e a força resistente como mostra a figura . Como exemplo temos o pegador de gelo, que é uma associação de alavancas interpotentes. | ||
| + | |||
| + | <br>Figuraxxx<br> | ||
| + | |||
| + | Figura xxxx | ||
| + | |||
| + | <br><br><br><br><br | ||
| + | |||
| + | ==Exercícios Conceituais== | ||
| + | |||
| + | '''1-''' Uma maquina é capaz de multiplicar a força aplicada sobre ela? Se sim, explique em que condições isso acontece.<br> | ||
| + | '''2-''' Uma alavanca é capaz de multiplicar a distância ao longo do qual atua uma força?<br> | ||
| + | '''3-''' Uma máquina é capaz de multiplicar energia e o trabalho que é fornecida?<br> | ||
| + | '''4-'''Classifique os tipos de alavanca [3]:<br> | ||
| + | |||
| + | [[Arquivo:Figura11.jpg|center]] | ||
| + | [[Arquivo:Figura12.jpg|center]] | ||
| + | [[Arquivo:Figura13.jpg|center]] | ||
| + | [[Arquivo:Figura14.jpg|center]] | ||
| + | [[Arquivo:Figura15.jpg|center]] | ||
| + | |||
| + | '''Respostas esperadas'''<br> | ||
| + | '''1-''' Sim, uma maquina pode aumentar, diminuir ou só mudar a direção de uma força aplicada sobre ela, a força é multiplicada quando a distância da força aplicada até o ponto de apoio é maior que a distância do ponto de apoio a carga (força resistente) a ser levantada. | ||
| + | |||
| + | '''2-''' Sim, pois para uma alavanca em equilíbrio termos: para um mesmo torque {<math>\tau=|F|.|r|.\sin(\theta)</math>}, temos que quanto menor a força aplicada maior o braço torçor. | ||
| + | |||
| + | '''3-''' A energia e o trabalho que é fornecido não podem ser multiplicados, pois se fossem violariam o principio de conservação de energia. | ||
| + | |||
| + | '''4-'''<br>'''a-''' Interfixa<br> | ||
| + | '''b-''' Inter-resistentes<br> | ||
| + | '''c-''' Interpotentes<br> | ||
| + | '''d-''' Interpotentes<br> | ||
| + | '''e-''' Interfixa<br> | ||
| + | '''f-''' Inter-resistente<br> | ||
| + | '''g-''' Interfixa<br> | ||
| + | '''h-''' Interpotentes<br> | ||
| + | '''i-''' inter-resistentes<br> | ||
| + | |||
| + | ==Atividade== | ||
| + | |||
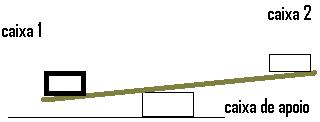
| + | Dado: caixas de fósforo, palitos de sorvete e 10 massas de mesmo peso (moedas, porcas) montar uma alavanca como da figura[1].<br> | ||
| + | [[Arquivo:Figura 7.jpg|left|'''Figura 7''']] | ||
| + | |||
| + | Variando os pesos das caixinhas e a distância delas a caixa de apoio responda as questões abaixo:<br> | ||
| + | :'''a-''' Comentar o que foi verificado experimentalmente.<br> | ||
| + | :'''b-''' Explicar porque a caixa mais leve consegue levantar a mais pesada.<br> | ||
| + | :'''c-''' Dar exemplos de alavancas que são usadas no dia-a-dia.<br><br><br> | ||
| + | |||
| + | '''Respostas esperadas'''<br> | ||
| + | '''a-''' Quando o ponto de apoio (caixa de apoio) está no meio da alavanca e o peso da caixinha 1 é igual ao peso da caixinha 2 elas se equilibram, pois a quantidade de esforço que você empurra para baixo é exatamente igual á quantidade de carga que você pode levantar com a outra extremidade.Já quando o peso das caixinhas são diferentes e o ponto de apoio se encontra no meio, a caixinha mais pesada levanta e desequilibra a outra para seu lado. No entanto quando a caixinha 1 está mais próxima do ponto de apoio a outra caixinha consegue levantar ela quando tem o mesmo peso dela e menor peso.<br> | ||
| + | '''b-''' A caixinha mais leve consegue levantar a mais pesada por ter distância maior ao ponto de apoio, assim ela necessita de uma força menor aplicada para levantar a outra caixinha.<br> | ||
| + | '''c-''' Como exemplo de alavancas podemos citar: macaco hidráulico, pé-de-cabra,alicate, chave de fenda, chave de boca,espremedor de batatas, ante-braço e etc.<br> | ||
| + | |||
| + | ==Problemas== | ||
| + | |||
| + | '''1-'''Suponha que você use como alavanca uma barra de 1,80m de comprimento com o ponto de apoio numa extremidade. Que massa colocada a 30 cm do ponto de apoio você pode levantar com uma força potente de 400N?[5]<br> | ||
| + | |||
| + | '''2-'''Uma noz é colocada a 2 cm da dobradiça de um quebra-nozes. Se você exerce uma força de 50N num ponto a 15cm da dobradiça, que força de resistência a noz exerce?[5]<br> | ||
| + | |||
| + | '''3-'''Suponha que numa pescaria você queira determinar o peso de um peixe e que você saiba que sua vara de pescar pesa 400g o que você faria?[5] | ||
| + | |||
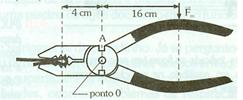
| + | '''4-'''O alicate da figura 2 é usado para dobrar fio de cobre. A força motriz aplicada pela pessoa vale 60N. [4]<br> | ||
| + | [[Arquivo:Figura8.jpg|left|'''Figura 7''']] <br> | ||
| + | ::::a- Qual a intensidade da força que comprime o fio?<br> | ||
| + | ::::b- Qual a vantagem mecânica do alicate?<br> | ||
| + | ::::c- Por que a posição do corte fica mais próxima da articulação?<br><br><br> | ||
| + | |||
| + | '''Respostas'''<br> | ||
| + | <br> | ||
| + | '''1-'''<math>Fp\times BP=Fr\times Br\ \ \ \Rightarrow Fr\times 0,3m=400N\times 1,8m \Rightarrow Fr=2400N\ \ que\ \ corresponde\ \ a\ \ 240Kg</math><br> | ||
| + | |||
| + | '''2-'''<math>Fp\times BP=Fr\times Br\ \ \ \Rightarrow Fr\times 2cm=50N\times 15cm \Rightarrow Fr=375N</math><br> | ||
| + | |||
| + | '''3-'''Você determina primeiro o centro de gravidade da vara equilibrando-a sobre a aresta de um canivete. Depois pendure o peixe numa das extremidades da vara. Deslize então a vara para frente e para trás sobre um suporte até equilibrá-la (Figura-xxxxx). Admita que o peso da vara atue no seu centro de gravidade. Meça o braço de alavanca AB da força potente exercida pelo peso da vara; meça o braço de alavanca BO da força resistente exercida pelo peixe (seu peso). Finalmente calcule o peso do peixe pela relação:<br> | ||
| + | ::::::Peso do peixe X braço BC = Peso da vara X braço AB.<br> | ||
| + | '''4-'''::<br> | ||
| + | |||
| + | ::a)O alicate é uma associação de alavancas. Ao se apertar o alicate no cabo surge na ponta uma força oposta, que faz com que o fio seja rompido. <br> | ||
| + | [[Arquivo:Figura9.jpg|center|'''Figura 7''']]<br> | ||
| + | ::Como a alavanca está em equilíbrio temos: <br> | ||
| + | [[Arquivo:Figura10.jpg|center|'''Figura 7''']]<br> | ||
| + | ::b) <math>vantagem\;\;mec.= \frac{Fr}{Fp}=\frac{240}{60}=4</math> | ||
| + | |||
| + | |||
| + | ::c) Porque, quanto menor a distância do corte até a articulação, maior será a força resistente isto é, maior será a vantagem mecânica. | ||
| + | |||
| + | ==Bibliografias== | ||
| + | Física conceitual<br> | ||
| + | Halliday<br> | ||
| + | [1] WWW.microsoft.com/Brasil/educação/default.mspx<br> | ||
| + | [2] http://pion.sbfisica.org.br/pdc/index.php/por/multimidia/simulacoes/mecanica<br> | ||
| + | [3] WWW.feiradeciencias.com.br<br> | ||
| + | [4] Física fundamental –Bonjorno<br> | ||
| + | [5]http://www4.prossiga.br/lopes/prodcien/fisicanaescola/cap3-1.htm<br> | ||
| + | http://www.fisica.net<br> | ||
| + | http://www.revistazoom.com.br<br> | ||
Edição atual tal como às 21h19min de 21 de setembro de 2009
Conteúdo[ocultar] |
[editar] Introdução
Este trabalho tem como objetivo dar fundamentos de alavancas a alunos do Ensino Médio usando experiências, simulações, experimentos pensados e textos. Procuramos dar um enfoque em situações cotidianas do dia-a-dia como uma forma de introduzir ao aluno o conceito de torque sem que este estivesse fora do contexto de sua vivência atual. O proposta se constitui na reprodução do trabalho final da discipina FGE0461 - Tecnologia de Ensino de Física I, produzido pela aluna Josiane Vieira Martins, que também é uma das contribuidoras na elaboração deste artigo.
[editar] Sobre a proposta
Aquí não é necessário o papel do professor, espera-se que: após o aluno que atenda os pré-requisitos fizer todas as atividades na ordem que aparece ele saiba explicar os ítens expressos no tópico 6. Nos tópicos 8, 9 e 10 colocamos respectivamente exercícios conceituais, atividade e problemas junto com as respostas esperadas para que o aluno possa testar seus conhecimentos.
[editar] Especificação da População Alvo
- Alunos do Ensino Médio
- Alunos cursando o final do 2º semestre do 1º ano
[editar] Pré-Requisitos
[editar] Seleção dos Conteúdos que serão abordados
- Máquinas Simples
- Alavanca
[editar] Ao final das atividades espera-se que o aluno saiba:
- Explicar como uma máquina é capaz de multiplicar a força aplicada sobre ela.
- Explicar o que acontece com a distância ao longo do qual atua uma força em uma alavanca.
- Explicar o que acontece com a energia e o trabalho fornecidos em uma alavanca.
- Descrever o funcionamento e dar exemplos de alavancas.
- Diferenciar os tipos de alavancas.
- Resolver problemas que envolvam alavancas.
[editar] Seqüência de Aprendizagem
[editar] Texto 1
|
|---|
Este texto vai permitir que ao final dele você possa estar entendendo a citação de Arquimedes e o que acontece na figura 1. Com a evolução, o homem criou instrumentos para facilitar as suas atividades de coleta, pesca e caça que facilitavam ou ampliava sua força, esses instrumentos são chamados de máquinas simples. Dentre as máquinas simples a mais comum é alavanca. Uma alavanca é uma barra que pode girar em torno de um ponto de apoio, temos que a alavanca é constituída de: ponto de apoio, força potente, força resistente, braço da força potente e braço da força resistente. Sendo que o braço da força potente é a distância do ponto que esta sendo aplicado a força potente ao ponto de apoio e o braço da força resistente é a distancia que esta sendo aplicada a força resistente ao ponto de apoio.
Sem as alavancas seria muito difícil fazer atividades como trocar o pneu do carro e tirar um parafuso.
[editar] Atividade 1
Verifique experimentalmente em que situação é necessário o uso de mais força:
- Abrir uma porta aplicando a força o mais próximo possível do eixo da maçaneta e depois o mais
longe possível. - Girar uma porca usando a mão e usando uma chave de boca.
- Abrir uma porta aplicando a força o mais próximo possível do eixo da maçaneta e depois o mais
Percebemos que temos que aplicar mais força quando: abrimos uma porta colocando a força mais próxima do eixo da maçaneta e giramos uma porca usando a mão, esses fatos tornam as propriedades de uma alavanca evidente, no qual as alavancas podem:
- Alterar a direção de uma força
- Aplicar uma força a distância
- Aumentar uma força
- Aumentar um movimento
[editar] Atividade 2
Utilizando o programa de simulação Princípio da Alavanca que está no seguinte endereço:
http://pion.sbfisica.org.br/pdc/index.php/por/content/view/full/447/(offset)/20
reproduza as situações abaixo e coloque os resultados na tabela1 e comente os resultados:
- força resistente = 2x força potente
braço resistente = braço potente - força resistente = 2x força potente
braço potente = 2x braço resistente - força resistente = 2x força potente
braço resistente = 2x braço potente
- força resistente = 2x força potente
| Força resistente x Braço Resistente | Força Potente x Braço Potente | |
|---|---|---|
| Situação 1 | _______________________________ | ___________________________ |
| Situação 2 | _______________________________ | ___________________________ |
| Situação 3 | _______________________________ | ___________________________ |
Tabela 1
Na simulação foi verificada que na situação 2, um peso menor consegue equilibrar um maior e pela tabela 1 podemos ver que os resultados dos produtos são iguais. Já nas situações 1 e 3 o produto do peso menor com seu braço é sempre menor que o produto do peso maior e seu braço, em que foi observado que o peso maior levanta o menor como também desequilibra a alavanca para seu lado.
Na simulação vimos que para levantar um peso maior utilizando um peso menor alteramos a distância entre a força e o ponto de apoio (situação 2), assim podemos dizer que o efeito de uma alavanca depende da força aplicada e do braço da força, esse efeito é chamado de momento de uma força, que é o produto das forcas pelos braços que foram colocados na Tabela 1. Podemos observar pela tabela 1 que na situação 2 onde houve equilíbrio os momentos são iguais, isso acontece porque quando uma alavanca está no equilíbrio o torque de um lado da alavanca é igual ao outro.
[editar] Texto 2
Temos que para sabermos a vantagem de uma alavanca usamos a seguinte relação:
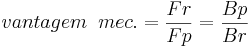
Equação 1
Onde: Fr = força resistente; Fp = força potente; Br = braço resistente; Bp = braço potente.
As alavancas são classificadas como interfixas, inter-resistentes e interpotente.
[editar] Alavanca interfixa
Como exemplo de alavanca interfixa temos a tesoura, que é uma associação de alavancas interfixas que é mostrada na Figura.
[editar] Alavanca Inter-Resistente
O martelo é um exemplo de alavanca inter-resistente.
[editar] Alavanca Interpotente
Temos que a força potente está entre o ponto de apoio e a força resistente como mostra a figura . Como exemplo temos o pegador de gelo, que é uma associação de alavancas interpotentes.
Figuraxxx
Figura xxxx
<br
[editar] Exercícios Conceituais
1- Uma maquina é capaz de multiplicar a força aplicada sobre ela? Se sim, explique em que condições isso acontece.
2- Uma alavanca é capaz de multiplicar a distância ao longo do qual atua uma força?
3- Uma máquina é capaz de multiplicar energia e o trabalho que é fornecida?
4-Classifique os tipos de alavanca [3]:
Respostas esperadas
1- Sim, uma maquina pode aumentar, diminuir ou só mudar a direção de uma força aplicada sobre ela, a força é multiplicada quando a distância da força aplicada até o ponto de apoio é maior que a distância do ponto de apoio a carga (força resistente) a ser levantada.
2- Sim, pois para uma alavanca em equilíbrio termos: para um mesmo torque {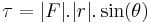 }, temos que quanto menor a força aplicada maior o braço torçor.
}, temos que quanto menor a força aplicada maior o braço torçor.
3- A energia e o trabalho que é fornecido não podem ser multiplicados, pois se fossem violariam o principio de conservação de energia.
4-
a- Interfixa
b- Inter-resistentes
c- Interpotentes
d- Interpotentes
e- Interfixa
f- Inter-resistente
g- Interfixa
h- Interpotentes
i- inter-resistentes
[editar] Atividade
Dado: caixas de fósforo, palitos de sorvete e 10 massas de mesmo peso (moedas, porcas) montar uma alavanca como da figura[1].
Variando os pesos das caixinhas e a distância delas a caixa de apoio responda as questões abaixo:
- a- Comentar o que foi verificado experimentalmente.
- b- Explicar porque a caixa mais leve consegue levantar a mais pesada.
- c- Dar exemplos de alavancas que são usadas no dia-a-dia.
Respostas esperadas
a- Quando o ponto de apoio (caixa de apoio) está no meio da alavanca e o peso da caixinha 1 é igual ao peso da caixinha 2 elas se equilibram, pois a quantidade de esforço que você empurra para baixo é exatamente igual á quantidade de carga que você pode levantar com a outra extremidade.Já quando o peso das caixinhas são diferentes e o ponto de apoio se encontra no meio, a caixinha mais pesada levanta e desequilibra a outra para seu lado. No entanto quando a caixinha 1 está mais próxima do ponto de apoio a outra caixinha consegue levantar ela quando tem o mesmo peso dela e menor peso.
b- A caixinha mais leve consegue levantar a mais pesada por ter distância maior ao ponto de apoio, assim ela necessita de uma força menor aplicada para levantar a outra caixinha.
c- Como exemplo de alavancas podemos citar: macaco hidráulico, pé-de-cabra,alicate, chave de fenda, chave de boca,espremedor de batatas, ante-braço e etc.
[editar] Problemas
1-Suponha que você use como alavanca uma barra de 1,80m de comprimento com o ponto de apoio numa extremidade. Que massa colocada a 30 cm do ponto de apoio você pode levantar com uma força potente de 400N?[5]
2-Uma noz é colocada a 2 cm da dobradiça de um quebra-nozes. Se você exerce uma força de 50N num ponto a 15cm da dobradiça, que força de resistência a noz exerce?[5]
3-Suponha que numa pescaria você queira determinar o peso de um peixe e que você saiba que sua vara de pescar pesa 400g o que você faria?[5]
4-O alicate da figura 2 é usado para dobrar fio de cobre. A força motriz aplicada pela pessoa vale 60N. [4]
- a- Qual a intensidade da força que comprime o fio?
- b- Qual a vantagem mecânica do alicate?
- c- Por que a posição do corte fica mais próxima da articulação?
- a- Qual a intensidade da força que comprime o fio?
Respostas
1-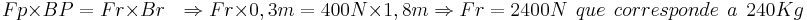
2-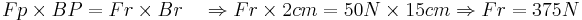
3-Você determina primeiro o centro de gravidade da vara equilibrando-a sobre a aresta de um canivete. Depois pendure o peixe numa das extremidades da vara. Deslize então a vara para frente e para trás sobre um suporte até equilibrá-la (Figura-xxxxx). Admita que o peso da vara atue no seu centro de gravidade. Meça o braço de alavanca AB da força potente exercida pelo peso da vara; meça o braço de alavanca BO da força resistente exercida pelo peixe (seu peso). Finalmente calcule o peso do peixe pela relação:
- Peso do peixe X braço BC = Peso da vara X braço AB.
- Peso do peixe X braço BC = Peso da vara X braço AB.
4-::
- a)O alicate é uma associação de alavancas. Ao se apertar o alicate no cabo surge na ponta uma força oposta, que faz com que o fio seja rompido.
- a)O alicate é uma associação de alavancas. Ao se apertar o alicate no cabo surge na ponta uma força oposta, que faz com que o fio seja rompido.
- Como a alavanca está em equilíbrio temos:
- Como a alavanca está em equilíbrio temos:
- b)

- b)
- c) Porque, quanto menor a distância do corte até a articulação, maior será a força resistente isto é, maior será a vantagem mecânica.
[editar] Bibliografias
Física conceitual
Halliday
[1] WWW.microsoft.com/Brasil/educação/default.mspx
[2] http://pion.sbfisica.org.br/pdc/index.php/por/multimidia/simulacoes/mecanica
[3] WWW.feiradeciencias.com.br
[4] Física fundamental –Bonjorno
[5]http://www4.prossiga.br/lopes/prodcien/fisicanaescola/cap3-1.htm
http://www.fisica.net
http://www.revistazoom.com.br