Mudanças entre as edições de "Teced/textos/Grupo 3"
Francislainy (disc | contribs) |
Fabianofan (disc | contribs) |
||
| Linha 91: | Linha 91: | ||
[[as:বেগ]] | [[as:বেগ]] | ||
[[be:Хуткасць]] | [[be:Хуткасць]] | ||
| − | |||
[[bg:Скорост]] | [[bg:Скорост]] | ||
[[bn:গতিবেগ]] | [[bn:গতিবেগ]] | ||
[[ca:Velocitat]] | [[ca:Velocitat]] | ||
| − | |||
[[cs:Rychlost]] | [[cs:Rychlost]] | ||
[[cy:Cyflymder]] | [[cy:Cyflymder]] | ||
| Linha 108: | Linha 106: | ||
[[fa:سرعت برداری]] | [[fa:سرعت برداری]] | ||
[[fi:Nopeus]] | [[fi:Nopeus]] | ||
| − | |||
[[fr:Vitesse]] | [[fr:Vitesse]] | ||
| − | |||
[[fy:Snelheid]] | [[fy:Snelheid]] | ||
[[ga:Treoluas]] | [[ga:Treoluas]] | ||
| Linha 127: | Linha 123: | ||
[[jv:Kacepetan]] | [[jv:Kacepetan]] | ||
[[kk:Жылдамдық]] | [[kk:Жылдамдық]] | ||
| − | |||
[[km:ល្បឿន]] | [[km:ល្បឿន]] | ||
[[ko:속도]] | [[ko:속도]] | ||
| Linha 141: | Linha 136: | ||
[[oc:Velocitat]] | [[oc:Velocitat]] | ||
[[pl:Prędkość]] | [[pl:Prędkość]] | ||
| − | |||
| − | |||
[[qu:Utqa kay]] | [[qu:Utqa kay]] | ||
[[ro:Viteză]] | [[ro:Viteză]] | ||
[[ru:Скорость]] | [[ru:Скорость]] | ||
| − | |||
[[sh:Brzina]] | [[sh:Brzina]] | ||
[[simple:Velocity]] | [[simple:Velocity]] | ||
| Linha 163: | Linha 155: | ||
[[uz:Tezlik]] | [[uz:Tezlik]] | ||
[[vi:Vận tốc]] | [[vi:Vận tốc]] | ||
| − | |||
[[yi:גיכקייט]] | [[yi:גיכקייט]] | ||
[[zh:速度]] | [[zh:速度]] | ||
[[zh-min-nan:Sok-tō͘]] | [[zh-min-nan:Sok-tō͘]] | ||
Edição das 19h44min de 2 de setembro de 2012
Conteúdo[ocultar] |
Velocidade
Na física, velocidade relaciona a variação da posição no espaço em relação ao tempo, ou seja, qual a distância percorrida por um corpo num determinado intervalo temporal. É uma grandeza vetorial, possuindo direção, sentido e módulo, esse último chamado de rapidez e de dimensões [L][T]-1, sendo medida no SI em metros por segundo (m/s ou ms-1). Em geral, os símbolos da velocidade são v ou 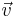 , o primeiro para a velocidade escalar e o segundo para o vetor velocidade.
A variação da velocidade em relação ao tempo é a aceleração.
, o primeiro para a velocidade escalar e o segundo para o vetor velocidade.
A variação da velocidade em relação ao tempo é a aceleração.
Equações de velocidade
Velocidade é um conceito fundamental para a mecânica clássica. Foi a partir desse que os primeiros físicos puderam desenvolver o estudo do movimento dos corpos, tornando-se capazes de descrever trajetórias através de funções matemáticas. Isaac Newton, pai da mecânica clássica, desenvolveu o cálculo diferencial a partir desse estudo. Há dois tipos de movimentos considerados mais simples: o movimento retilíneo uniforme(MRU) e o movimento retílineo uniformemente variado(MRUV), que são representados por equações lineares e quadrádicas respectivamente. Para outros tipos de movimento mais complexos utiliza-se a derivada.
Movimento Retílineo Uniforme
É o movimento descrito por objetos com velocidade constante, para tal, é preciso que a resultante das forças que atuam sobre o corpo seja nula. Dado um deslocamento  , em um tempo
, em um tempo  A velocidade escalar v é dada por:
A velocidade escalar v é dada por:
 .
.
Somente no MRU a velocidade de um corpo a qualquer instante é igual à sua velocidade média.
A equação do espaço S em função do tempo t, a partir de um ponto  é:
é:

O gráfico sxt desse movimento é uma linha reta cuja tangente do ângulo de inclinação dessa reta, em relação ao eixo t é o valor da velocidade.
Movimento Retilíneo Uniformemente Variado
É o movimento de objetos que variam sua velocidade de forma constante, ou seja, possuem aceleração constante.
No MRUV a equação da aceleração é análoga à da velocidade no MRU; e a equação de velocidade no MRUV é análoga à do espaço no MRU.


E a equação do espaço é a seguinte:

O gráfico sxt desse movimento é uma parábola.
Veja mais em movimento retilíneo.
Derivada
Os dois movimentos acima só ocorrem em condições muito especificas, para estudar os movimentos dos corpos como ocorrem na natureza Newton desenvolveu a derivada, para calcular a velocidade instantânea de um corpo em certo instante é necessário usar limite, medindo-se uma variação infinitesimal de espaço em um intervalo infinitesimal de tempo.

Da definição de derivada:

Com a derivação é possível calcular a velocidade de um objeto a partir do gráfico sxt, ela fornece a inclinação da reta tangente ao ponto na curva correspondente, sendo essa a velocidade instantânea.
A aceleração é a derivada da velocidade com relação ao tempo:

Unidades de velocidade
Sistema Internacional de Unidades (SI)
- Metro por segundo (m/s): unidade de velocidade do SI (1 m/s = 3,6 km/h).
Sistema CGS de unidades
- Centímetro por segundo (cm/s)
Sistema imperial de medidas
- Pé por segundo (ft/s)
- Milha por hora (mph)
- Milha por segundo (mps)
- O nó é uma unidade de medida da velocidade, utilizada na navegação marítima e aérea, equivalente a uma milha náutica por hora.
Aeronáutica
- Número de Mach. O Número de Mach (M) é uma medida de velocidade relativa que se define como o quociente entre a velocidade dum objeto e a velocidade do som no meio em que se move dito objeto. É um número adimensional tipicamente usado para descrever a velocidade dos aviões. Mach 1 equivale à velocidade do som; Mach 2 é duas vezes a velocidade do som; e assim sucessivamente. A velocidade do som no ar é de 340 m/s (1224 km/h).
Unidades naturais
- Velocidade da luz no vácuo = 299 792 458 m/s (convencionalmente 300 000 km/s). É a maior velocidade que se pode atingir no Universo segundo a Teoria Restrita da Relatividade de Einstein.
Outras unidades
- Quilômetro por hora (km/h)
- Quilômetro por segundo (km/s)