Mudanças entre as edições de "Usuário:Calsaverini/data"

De Stoa
Ir para: navegação, pesquisa
(Criou página com '== Expansão para função de partição em baixas temperaturas == Imagine que se quer calcular <math> \displaystyle Z = \sum_{x} e^{-\beta E(x)}</math> para <math>\beta = \fra…')
 
Linha 1: Linha 1:
 +
= Bobagens que não parecem chegar em lugar algum mas não saem da minha cabeça =
 
== Expansão para função de partição em baixas temperaturas ==
 
== Expansão para função de partição em baixas temperaturas ==
−
Imagine que se quer calcular  
+
Imagine que se quer calcular <math> \displaystyle Z = \sum_{x} e^{-\beta E(x)}</math> para <math>\beta = \frac{1}{T} \to\infty</math>. Escreva como <math> Z = \int e^{-E/T} \rho(E) dE </math>, onde <math> \rho(E) = \sum_{x} \delta(E - E(x))</math>. Note que:
−
<math> \displaystyle Z = \sum_{x} e^{-\beta E(x)}</math>  
+
−
para <math>\beta = \frac{1}{T} \to\infty</math>.  
+
  
−
write it as:
+
<math>\int e^{-\frac{Ax^2}{2}+ B x} dx = \sqrt{\frac{2\pi}{A}}e^{\frac{B^2}{2A}}</math>
  
−
rho(E) = \sum_{x} \delta(E - E(x))
+
Então, se <math>B = i\sqrt{2E}</math> e <math>\displaystyle T = A</math> temos <math> e^{-\frac{E}{T}} = \int du \exp\left[-\frac{T u^2}{2}- i\sqrt{2E} u\right] </math> e então:
  
−
Z = \int exp(-E/T) rho(E) dE
+
<math> Z = \int du\; e^{-\frac{Tu^2}{2}} \int dE \; e^{-i\sqrt{2E} u} \rho(E) </math>
  
 +
vamos chamar <math> \Xi(u) = \int dE e^{-i\sqrt{2E}u} \rho(E)</math> e fazer a mudança de variáveis <math>E = \frac{p^2}{2}</math> então:
 +
<math> \Xi(u) = \int p dp\; e^{-ipu} \rho\left(\frac{p^2}{2}\right)</math>
  
 +
Se me interesso por <math> T \to 0</math>, posso expandir em série de potências:
  
−
note that: \int exp(-1/2 A x² + B x) dx = sqrt(2\pi/A) exp(1/2 B² / A)
+
<math> Z = \int du\; e^{-\frac{T u^2}{2}} \Xi(u) </math>
  
−
So, if E = -B²/2 (B = i\sqrt{2E} ) and T = A we have
+
<math> = \int du\;\Xi(u) \sum_{n=0}^{\infty} \frac{(-1)^n T^n u^{2n}}{n!}</math>
 +
<math> = \sum_{n=0}^{\infty} \frac{(-1)^n T^n}{n!} \int du\;\Xi(u) u^{2n}</math>
  
−
exp(-E/T) = \int du exp(-1/2 T u² - i\sqrt{2E} u)  
+
<math> = \int du \;\Xi(u)- \frac{1}{2} T \int du \;\Xi(u) u^2 + \ldots</math>
  
−
and then:
 
  
 +
Mas <math> \Xi(u)</math> está na forma de uma transformada de Fourier, <math> \Xi(u) = \int dp\; e^{-ipu} F(p)</math>, com <math>F(p) = p \rho\left(\frac{p^2}{2}\right)</math>
  
−
Z = \int du exp(-1/2 T u²) \int dE exp(-i\sqrt{2E} u) \rho(E)
+
E então podemos escrever:
  
−
call Chi(u) = \int dE exp(-i\sqrt{2E}u) \rho(E)  
+
<math>\int du\;\Xi(u) u^{2n} = \int du\,dp\; F(p) e^{-ipu} u^{2n}</math>
 +
<math> = \int dp F(p)(-i\partial_p)^{2n}\delta(p) = (-1)^n F^{2n}(0)</math>
  
−
and make a change of variables
+
E então:
−
p = \sqrt{2E}
+
−
E = p²/2  dE = p dp
+
  
−
then:
+
<math>Z =  \sum_{n=0}^{\infty} \frac{ F_{n}}{n!} T^n </math>
  
−
Chi(u) = \int dp exp(-ipu) p\rho(p²/2)  
+
onde <math> \displaystyle F_{n} = \lim_{p\to 0} \frac{d^{2n}}{dp^{2n}} \left[p \rho\left(\frac{p^2}{2}\right)\right]</math>
  
−
and call
+
lembrando a definição de <math> \rho(E)</math>:
  
−
\Rho(p) = p\rho(p²/2)  = p \sum_{x} \delta(p²/2 - E(x))
+
<math> \displaystyle F_{n} = \lim_{p\to 0} \frac{d^{2n}}{dp^{2n}} \left[p \sum_{x} \delta\left(\frac{p^2}{2} - E(x)\right)\right]</math>
−
 
+
−
If I'm interested in T -> 0 then I can expand Z in powers of T:
+
−
 
+
−
Z = \int du exp(-1/2 T u²) \tilde{\Rho}(u)
+
−
 
+
−
= \int du \tilde{\Rho}(u) \left(1 - 1/2 T u² + ...\right)
+
−
 
+
−
= \int du \tilde{\Rho}(u) - 1/2 T u² \int du \tilde{\Rho}(u) u²
+
−
 
+
−
 
+
−
\tilde{\Rho}(u)  = \int dp exp(-ipu) \Rho(p)
+
−
 
+
−
\int du \tilde{\Rho}(u) = \Rho(0) = lim_{p->0} p \sum{x} \delta(p²/2 - E(x))
+
−
\int du u² \tilde{\Rho}(u) = \Rho''(0)
+
−
 
+
−
 
+
−
Z = \Rho(0) - T/2 \Rho''(0) + O(T²)
+

Edição das 16h39min de 12 de setembro de 2010

Bobagens que não parecem chegar em lugar algum mas não saem da minha cabeça

Expansão para função de partição em baixas temperaturas

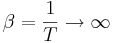Imagine que se quer calcular \displaystyle Z = \sum_{x} e^{-\beta E(x)} para \beta = \frac{1}{T} \to\infty. Escreva como 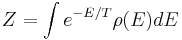Z = \int e^{-E/T} \rho(E) dE , onde 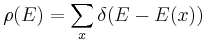\rho(E) = \sum_{x} \delta(E - E(x)). Note que:

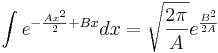
\int e^{-\frac{Ax^2}{2}+ B x} dx = \sqrt{\frac{2\pi}{A}}e^{\frac{B^2}{2A}}

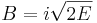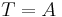Então, se B = i\sqrt{2E} e \displaystyle T = A temos e^{-\frac{E}{T}} = \int du \exp\left[-\frac{T u^2}{2}- i\sqrt{2E} u\right] e então:

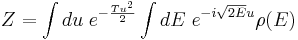
Z = \int du\; e^{-\frac{Tu^2}{2}} \int dE \; e^{-i\sqrt{2E} u} \rho(E)

vamos chamar \Xi(u) = \int dE e^{-i\sqrt{2E}u} \rho(E) e fazer a mudança de variáveis E = \frac{p^2}{2} então: \Xi(u) = \int p dp\; e^{-ipu} \rho\left(\frac{p^2}{2}\right)

Se me interesso por T \to 0, posso expandir em série de potências:

Z = \int du\; e^{-\frac{T u^2}{2}} \Xi(u)

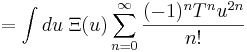
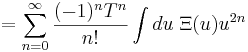
= \int du\;\Xi(u) \sum_{n=0}^{\infty} \frac{(-1)^n T^n u^{2n}}{n!} = \sum_{n=0}^{\infty} \frac{(-1)^n T^n}{n!} \int du\;\Xi(u) u^{2n}

= \int du \;\Xi(u)- \frac{1}{2} T \int du \;\Xi(u) u^2 + \ldots


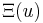Mas \Xi(u) está na forma de uma transformada de Fourier, 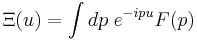\Xi(u) = \int dp\; e^{-ipu} F(p), com F(p) = p \rho\left(\frac{p^2}{2}\right)

E então podemos escrever:

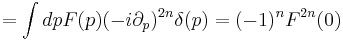
\int du\;\Xi(u) u^{2n} = \int du\,dp\; F(p) e^{-ipu} u^{2n} = \int dp F(p)(-i\partial_p)^{2n}\delta(p) = (-1)^n F^{2n}(0)

E então:

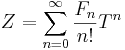
Z = \sum_{n=0}^{\infty} \frac{ F_{n}}{n!} T^n

onde \displaystyle F_{n} = \lim_{p\to 0} \frac{d^{2n}}{dp^{2n}} \left[p \rho\left(\frac{p^2}{2}\right)\right]

lembrando a definição de \rho(E):

\displaystyle F_{n} = \lim_{p\to 0} \frac{d^{2n}}{dp^{2n}} \left[p \sum_{x} \delta\left(\frac{p^2}{2} - E(x)\right)\right]

Disponível em "http://wiki.stoa.usp.br/index.php?title=Usuário:Calsaverini/data&oldid=12685"
Ferramentas pessoais

Variantes
Ações
Navegação
Imprimir/exportar
Ferramentas