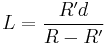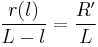Mudanças entre as edições de "Teced/textos/grupo30"
| Linha 55: | Linha 55: | ||
==Referências== | ==Referências== | ||
<references/> | <references/> | ||
| − | + | [http://astro.if.ufrgs.br/eclipses/eclipse.htm Measurement of physics] | |
== Grupo colaborador == | == Grupo colaborador == | ||
[[:pt:Laís Marina Banov|Laís Marina Banov]]<br /> | [[:pt:Laís Marina Banov|Laís Marina Banov]]<br /> | ||
[[:pt:Francisco Soares de Oliveira|Francisco Soares de Oliveira]] (soaresmontanha@gmail.com) | [[:pt:Francisco Soares de Oliveira|Francisco Soares de Oliveira]] (soaresmontanha@gmail.com) | ||
Edição das 10h47min de 23 de outubro de 2014
Eclipse
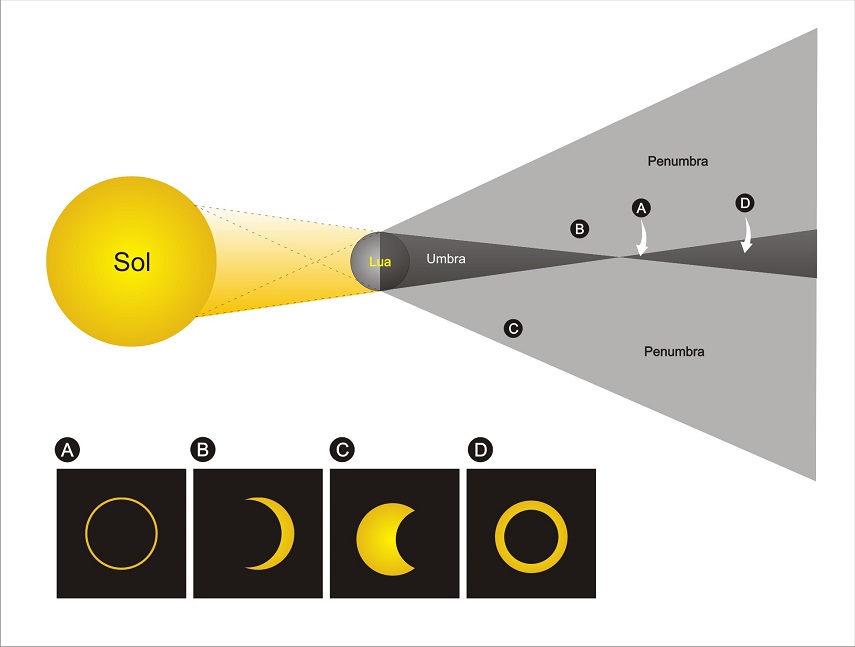
Eclipse é a ocultação da visão de um corpo, quando este entra na sombra(umbra) de outro corpo. Então,quando a Lua entra na sombra da Terra, ocorre o eclipse lunar. E quando a Terra entra na sobra da Lua temos o eclipse solar.
[1]
Conteúdo[ocultar] |
Geometria da sombra
A iluminação de um corpo extenso opaco por uma corpo extenso com luz própria(fonte) define três regiões de sombra:
- umbra: região da sombra com ausência de luz, a qual é completamente obstruída pelo corpo opaco. Um observador situado nesta região verifica um eclipse total da fonte.
- penumbra: região da sombra na qual apenas uma parte da fonte é obscurecida pelo corpo opaco. A partir desta região observa-se um eclipse parcial da fonte. O corpo opaco é observado parcialmente dentro da secção transversal da fonte observada.
- antumbra: região da sombra parcialmente iluminada e a partir da qual um observador verifica o corpo opaco totalmente dentro da secção transversal da fonte observada. Observa-se nesta região o eclipse anular.
Cálculo do comprimento da sombra
Consideremos um corpo luminoso esférico de raio R a uma distância d de uma esfera opaca de raio R'. A umbra originada a partir do corpo opaco tem o formato de um cone, cuja altura é o tamanho da sombra.

Sendo:
- L = comprimento do cone de sombra, isto é, comprimento da umbra em formato de cone
- d = distância da fonte ao corpo opaco
- R = raio da fonte luminosa esférica
- R' = raio da esfera opaca
Por semelhança de triângulos temos que:
E portanto a altura do cone de sombra (L) é:
Cálculo do raio da sombra
A seguir vamos determinar o tamanho da sombra a uma certa distância l da esfera opaca. Como a sombra é cônica, sua forma em qualquer onto é circular.
Sendo:
- r(l) = raio da sombra à distância l da esfera opaca
- L = comprimento da sombra
- R' = raio da esfera opaca
Novamente por semelhança de triângulos temos que:
E o raio da sombra à distância l da esfera opaca é:
Referências
Grupo colaborador
Laís Marina Banov
Francisco Soares de Oliveira (soaresmontanha@gmail.com)