Usuário:Calsaverini/data

Expansão para função de partição em baixas temperaturas

Imagine que se quer calcular $\displaystyle Z = \sum_{x} e^{-\beta E(x)}$ para $\beta = \frac{1}{T} \to\infty$.

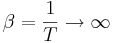write it as:

rho(E) = \sum_{x} \delta(E - E(x))

Z = \int exp(-E/T) rho(E) dE

note that: \int exp(-1/2 A x² + B x) dx = sqrt(2\pi/A) exp(1/2 B² / A)

So, if E = -B²/2 (B = i\sqrt{2E} ) and T = A we have

exp(-E/T) = \int du exp(-1/2 T u² - i\sqrt{2E} u)

and then:

Z = \int du exp(-1/2 T u²) \int dE exp(-i\sqrt{2E} u) \rho(E)

call Chi(u) = \int dE exp(-i\sqrt{2E}u) \rho(E)

and make a change of variables p = \sqrt{2E} E = p²/2 dE = p dp

then:

Chi(u) = \int dp exp(-ipu) p\rho(p²/2)

and call

\Rho(p) = p\rho(p²/2) = p \sum_{x} \delta(p²/2 - E(x))

If I'm interested in T -> 0 then I can expand Z in powers of T:

Z = \int du exp(-1/2 T u²) \tilde{\Rho}(u)

= \int du \tilde{\Rho}(u) \left(1 - 1/2 T u² + ...\right)

= \int du \tilde{\Rho}(u) - 1/2 T u² \int du \tilde{\Rho}(u) u²

\tilde{\Rho}(u) = \int dp exp(-ipu) \Rho(p)

\int du \tilde{\Rho}(u) = \Rho(0) = lim_{p->0} p \sum{x} \delta(p²/2 - E(x)) \int du u² \tilde{\Rho}(u) = \Rho(0)

Z = \Rho(0) - T/2 \Rho(0) + O(T²)