Map2313
Conteúdo[ocultar] |
Tópicos de Matemática Aplicada [1]
Resumo das duas primeiras aulas
Nesta disciplina, uma equação a derivadas parciais (EDP) é uma relação entre uma variável dependente real ( ) e variáveis independentes
(duas ou mais) e as derivadas parciais de
) e variáveis independentes
(duas ou mais) e as derivadas parciais de  com relação às suas variáveis independentes.
com relação às suas variáveis independentes.
Exemplos
O primeiro exemplo é uma equação linear de primeira ordem. O segundo exemplo é uma equação de primeira ordem as não linear.
A ordem de uma EDP é o número de derivadas do termo em  que tem o maior número de derivadas.
Se a relação que determina a EDP puder ser escrita como uma soma algébrica de termos
que tem o maior número de derivadas.
Se a relação que determina a EDP puder ser escrita como uma soma algébrica de termos

e em cada um destes termos  aparece apenas
aparece apenas  ou uma derivada parcial de
ou uma derivada parcial de  de qualquer ordem multiplicada
por um fator que pode ou não depender das variáveis independentes, diremos que esta equação é linear. Nesta disciplinas nos ocuparemso de algumas equações a derivadas parciais lineares que aparecem na matemática aplicada.
de qualquer ordem multiplicada
por um fator que pode ou não depender das variáveis independentes, diremos que esta equação é linear. Nesta disciplinas nos ocuparemso de algumas equações a derivadas parciais lineares que aparecem na matemática aplicada.
Resolver uma EDP é encontrar a relação de  com suas variáveis independentes de modo que se verifique a equação dada. De forma geral existem muitas soluções e além da equação, propriamente dita, são dadas outras condições complementares para a variável
com suas variáveis independentes de modo que se verifique a equação dada. De forma geral existem muitas soluções e além da equação, propriamente dita, são dadas outras condições complementares para a variável  chamadas condições de contorno.
chamadas condições de contorno.
O conjunto das soluções de uma EDP linear homogênea tem a propriedade da linearidade ou superposição: a soma de duas soluções é uma solução e o multiplo por um escalar de uma solução é outra solução.
Equação da corda vibrante
Na segunda aula fizemos a dedução da equação e uma corda vibrante

onde  Supondo tensão na corda
Supondo tensão na corda  e densidade da corda
e densidade da corda  constantes.
constantes.
Condições de fronteira para a corda vibrante

Soluções de Equações a derivadas parciais
--Patonelli 22h10min de 6 de Março de 2009 (UTC)
Informações administrativas para o primeiro semestre de 2009
Docente : Pedro Aladar Tonelli
Provas : 7 de maio, 25 de junho e 2 de Julho
Média final:  onde
onde  é a média das duas melhores provas e
é a média das duas melhores provas e 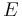 é a média das listas de exercícios.
é a média das listas de exercícios.
Bibliografia:
E Kreysig Matemática superior D G Figueiredo Análise de Fourier e Equações Diferenciais Parciais
--Patonelli 14h12min de 16 de Fevereiro de 2009 (UTC)Pedro A Tonelli


