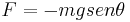Mudanças entre as edições de "Fap0459/textos/grupo Marcelo/Debora/Rafael/Diogo"
(→Introdução Teórica) |
(→Introdução Teórica) |
||
| Linha 12: | Linha 12: | ||
Para pequenos deslocamentos, ou seja, para valores pequenos do ângulo de abertura (ângulo entre a vertical e o fio inextensível), a força resultante é proporcional ao deslocamento, porém de sentido oposto. Tal característica representa o movimento harmônico simples, daí, portanto pode se deduzir a fórmula do período do movimento. | Para pequenos deslocamentos, ou seja, para valores pequenos do ângulo de abertura (ângulo entre a vertical e o fio inextensível), a força resultante é proporcional ao deslocamento, porém de sentido oposto. Tal característica representa o movimento harmônico simples, daí, portanto pode se deduzir a fórmula do período do movimento. | ||
Para facilitar, escolhe-se um sistema de referência com um dos eixos tangencial à trajetória do pêndulo e o outro perpendicular, ou seja, está na direção radial. | Para facilitar, escolhe-se um sistema de referência com um dos eixos tangencial à trajetória do pêndulo e o outro perpendicular, ou seja, está na direção radial. | ||
| − | Decompondo a força peso P, será obtido uma componente radial <math>{ | + | Decompondo a força peso P, será obtido uma componente radial <math>{mgcos\theta}</math> e outra tangencial <math>{mgsen\theta}</math>. |
A direção radial da força resultante é a força centrípeta necessária para manter a massa na ponta do fio na trajetória circular. Já na direção tangencial, a força é restauradora e faz com que a massa tende a retornar à posição de equilíbrio. | A direção radial da força resultante é a força centrípeta necessária para manter a massa na ponta do fio na trajetória circular. Já na direção tangencial, a força é restauradora e faz com que a massa tende a retornar à posição de equilíbrio. | ||
Esta força restauradora é dada por | Esta força restauradora é dada por | ||
<math>{F=-mgsen\theta}</math> | <math>{F=-mgsen\theta}</math> | ||
Edição das 20h49min de 3 de setembro de 2009
Experimento utilizando pêndulo simples
Os participantes do grupo são Débora, Diogo, Marcelo e Rafael
Objetivos da Experiência
O roteiro abaixo consiste de uma simples experiência com pêndulo simples para que se possa identificar as variáveis que influenciam no período de oscilação. Com este aparato é possível também calcular a aceleração gravidade no local onde o experimento é realizado. Faz parte do experimento a compreensão física das expressões envolvidas assim como os cálculos das incertezas que ocorrem nas medições.
Introdução Teórica
O pêndulo simples consiste num fio, considerado inextensível, tendo uma de suas extremidades fixada num certo ponto, e a outra com uma massa concentrada. Quando afastado de sua posição de equilíbrio e solto, o pêndulo realizará oscilações em torno do eixo de rotação sob ação da gravidade. Perceba que além da força peso há a tração aplicada da corda na massa em questão.
Seu movimento representa, portanto, um movimento oscilatório, de modo que haja uma periodicidade, que é o tempo para realizar uma oscilação.
Para pequenos deslocamentos, ou seja, para valores pequenos do ângulo de abertura (ângulo entre a vertical e o fio inextensível), a força resultante é proporcional ao deslocamento, porém de sentido oposto. Tal característica representa o movimento harmônico simples, daí, portanto pode se deduzir a fórmula do período do movimento.
Para facilitar, escolhe-se um sistema de referência com um dos eixos tangencial à trajetória do pêndulo e o outro perpendicular, ou seja, está na direção radial.
Decompondo a força peso P, será obtido uma componente radial 
e outra tangencial 
.
A direção radial da força resultante é a força centrípeta necessária para manter a massa na ponta do fio na trajetória circular. Já na direção tangencial, a força é restauradora e faz com que a massa tende a retornar à posição de equilíbrio.
Esta força restauradora é dada por
