Mudanças entre as edições de "Fap0459/textos/grupo Marcelo/Debora/Rafael/Diogo"
(→Introdução Teórica) |
|||
| (81 edições intermediárias de 4 usuários não apresentadas) | |||
| Linha 2: | Linha 2: | ||
Os participantes do grupo são Débora, Diogo, Marcelo e Rafael | Os participantes do grupo são Débora, Diogo, Marcelo e Rafael | ||
| + | |||
=== Objetivos da Experiência === | === Objetivos da Experiência === | ||
| − | O roteiro abaixo consiste de uma simples experiência com pêndulo simples para que se possa identificar as variáveis que influenciam no período de oscilação. Com este aparato é possível também calcular a aceleração gravidade no local onde o experimento é realizado. Faz parte do experimento a compreensão física das expressões envolvidas assim como os cálculos das incertezas que ocorrem nas medições. | + | O roteiro abaixo consiste de uma simples experiência com pêndulo simples para que se possa identificar as variáveis que influenciam no período de oscilação. Com este aparato é possível também calcular a aceleração gravidade no local onde o experimento é realizado. Faz parte do experimento a compreensão física das expressões envolvidas assim como os cálculos das [[:pt:incerteza|incertezas]] que ocorrem nas medições. |
=== Introdução Teórica === | === Introdução Teórica === | ||
| + | [[:pt:Galileu Galilei|Galileu Galilei]] desenvolveu os primeiros estudos sistemáticos do movimento uniformemente acelerado e do movimento do pêndulo. [[Arquivo:Galileo.jpg|thumb|right|'''Galileu Galilei'''<br/>Descobriu a lei dos corpos e enunciou o princípio da inércia e o conceito de referencial inercial, ideias precursoras da mecânica newtoniana. | ||
| + | O físico desenvolveu ainda vários instrumentos como o relógio de pêndulo.]] | ||
| + | O pêndulo simples consiste num fio, considerado inextensível, tendo uma de suas extremidades fixada num certo ponto, e a outra com uma massa concentrada. Quando afastado de sua posição de equilíbrio e solto, o pêndulo realizará oscilações em torno do eixo de rotação sob ação da [[:pt:gravidade|gravidade]]. Perceba que além da [[:pt:força peso|força peso]] há a tração aplicada da corda na massa em questão. | ||
| − | |||
Seu movimento representa, portanto, um movimento oscilatório, de modo que haja uma periodicidade, que é o tempo para realizar uma oscilação. | Seu movimento representa, portanto, um movimento oscilatório, de modo que haja uma periodicidade, que é o tempo para realizar uma oscilação. | ||
| − | Para pequenos deslocamentos, ou seja, para valores pequenos do ângulo de abertura (ângulo entre a vertical e o fio inextensível), a força resultante é proporcional ao deslocamento, porém de sentido oposto. Tal característica representa o movimento harmônico simples, daí, portanto pode se deduzir a fórmula do período do movimento. | + | Para pequenos deslocamentos, ou seja, para valores pequenos do ângulo de abertura (ângulo entre a vertical e o fio inextensível), a força resultante é proporcional ao deslocamento, porém de sentido oposto. Tal característica representa o [[:pt:MHS|movimento harmônico simples]], daí, portanto pode se deduzir a fórmula do [[:pt:período|período]] do movimento. |
| + | |||
Para facilitar, escolhe-se um sistema de referência com um dos eixos tangencial à trajetória do pêndulo e o outro perpendicular, ou seja, está na direção radial. | Para facilitar, escolhe-se um sistema de referência com um dos eixos tangencial à trajetória do pêndulo e o outro perpendicular, ou seja, está na direção radial. | ||
Decompondo a força peso P, será obtido uma componente radial <math>{mgcos\theta}</math> e outra tangencial <math>mgsen\theta</math>. | Decompondo a força peso P, será obtido uma componente radial <math>{mgcos\theta}</math> e outra tangencial <math>mgsen\theta</math>. | ||
| Linha 19: | Linha 23: | ||
Para ângulos muito pequenos, <math>\sin\theta \simeq \theta\,</math>, para o ângulo medido em radianos. | Para ângulos muito pequenos, <math>\sin\theta \simeq \theta\,</math>, para o ângulo medido em radianos. | ||
| − | Assim <math>{F = mg\theta}</math> | + | Assim <math>{F = mg\theta}</math> |
| − | Pela segunda Lei de Newton: <math>{md^2\theta\over dt^2}=-{mg} \theta. </math> | + | |
| + | Pela segunda Lei de Newton: <math>{md^2\theta\over dt^2}=-{mg} \theta. </math> [[Arquivo:pendulo1.gif|thumb|right|pêndulo simples]] | ||
Como <math>{\theta}={x\over L}</math> | Como <math>{\theta}={x\over L}</math> | ||
<math>{d^2x\over dt^2} = -{mgx\over L}</math> | <math>{d^2x\over dt^2} = -{mgx\over L}</math> | ||
| − | O termo <math>{mg\over L}</math> da expressão acima é constante e desempenha o mesmo papel da constante <math>{k}</math> usada no cálculo da velocidade angular de um movimento harmônico. | + | O termo <math>{mg\over L}</math> da expressão acima é constante e desempenha o mesmo papel da constante <math>{k}</math> usada no cálculo da [[:pt:Velocidade angular|velocidade angular]] de um movimento harmônico. |
Desta maneira: | Desta maneira: | ||
| Linha 37: | Linha 42: | ||
Igualando as duas expressões logo acima, obtém se o período de oscilação do pêndulo: | Igualando as duas expressões logo acima, obtém se o período de oscilação do pêndulo: | ||
| − | <math>T = {2\pi\sqrt{ | + | <math>T = {2\pi\sqrt{L\over g}}</math> |
Sendo conhecido o período de oscilação e o comprimento do fio, basta isolar g para que possa calculá-lo: | Sendo conhecido o período de oscilação e o comprimento do fio, basta isolar g para que possa calculá-lo: | ||
| − | <math>g = 4\{ | + | <math>g = {4\pi^2L\over T^2}</math> |
| + | |||
| + | ===Relação dos Materiais=== | ||
| + | #Bolinhas do pêndulo com as seguintes massas: | ||
| + | #*10g | ||
| + | #*33g | ||
| + | #*50g | ||
| + | #Fio inextensível | ||
| + | #Cronômetro | ||
| + | #Trena | ||
| + | <gallery> | ||
| + | Arquivo:pêndulo.jpg|Materiais | ||
| + | |||
| + | |||
| + | Arquivo:trena.jpg | ||
| + | Arquivo:cronometro.jpg | ||
| + | |||
| + | </gallery> | ||
| + | |||
| + | ===Descrição Experimental=== | ||
| + | O experimento do pêndulo simples consistirá em quatro procedimentos para verificação dos parâmetros que influenciam o período de oscilação (T) e o cálculo da aceleração da gravidade. | ||
| + | |||
| + | No primeiro procedimento, será observado se o período de oscilação depende do ângulo inicial. Utilizando uma bolinha de qualquer uma das massas e um fio com 65,5 cm de comprimento, deve se adotar ângulos iniciais de 5°, 10°, 15°, 20° e 30°. Meça com um cronômetro o tempo gasto de dez oscilações, obtendo o período de uma única oscilação utilizando o cálculo de média simples. Com os dados obtidos construa uma tabela (1) e um gráfico (1) de Tx <math>\theta</math> onde <math>\theta</math> é o ângulo de amplitude inicial. A partir dos dados, é possível calcular a incerteza (<math>\sigma_m</math>) de cada medida obtida, o valor médio (<math>T_m</math>) de oscilação e sua respectiva incerteza (<math>\sigma_{media}</math>). | ||
| + | |||
| + | No segundo procedimento, será verificado se o período de oscilação do pêndulo depende da massa do corpo, no caso a bolinha. Adotando um ângulo inicial de amplitude de 10° e um fio com 65,5 cm de comprimento, utiliza-se no experimento bolinhas com 10 g, 33 g e 50 g. Realizando o mesmo método anterior para obter o período médio de oscilação de cada situação, obtém-se novamente o período de uma oscilação (com a ajuda de um cronômetro). Construa uma tabela (2) com os dados e um gráfico (2) de TxM, onde M é a massa de cada bolinha. Com os dados obtidos, calcula-se a incerteza de cada medida de período (<math>\sigma_m</math>), o tempo médio de uma oscilação (<math>T_m</math>) e sua respectiva incerteza (<math>\sigma_{media}</math>). | ||
| + | |||
| + | No terceiro procedimento, será analisada a dependência do período de oscilação com o comprimento do fio. Utilizando uma das bolinhas e adotando um ângulo inicial de amplitude de 10°, muda-se o comprimento do fio em 30cm, 60cm e 90cm e execute o mesmo processo anterior para encontrar o período médio para cada uma das situações. Com os valores, monta-se outra tabela (3) e um respectivo gráfico, mas desta vez o gráfico não é de TxL e sim um de T²xL, pois assim, teoricamente, será encontrado uma reta, na qual o valor da aceleração da gravidade é extraído do coeficiente angular da mesma. Além disso, como das outras vezes, calcula-se as incertezas das medidas (<math>\sigma_m</math>), o valor do período médio (<math>T_m</math>) de uma oscilação e sua incerteza (<math>\sigma_{media}</math>). | ||
| + | |||
| + | O último procedimento é feito apenas para a determinação do valor da aceleração da gravidade através da expressão matemática apresentada anteriormente. Então usou-se novamente uma bolinha qualquer, um ângulo de amplitude de 10° e um fio com 50 cm de comprimento. Com a ajuda do cronômetro se faz a medida do período (a média calculada como nos outros procedimentos) e por fim o cálculo da aceleração da gravidade. | ||
| + | |||
| + | === Cálculos envolvidos no experimento === | ||
| + | |||
| + | Nos procedimentos 1,2 e 3, para o cálculo do período médio usa-se apenas uma média aritmética dos valores de períodos obtidos com a expressão: | ||
| + | <math>T_m = {\dfrac{1}n\sum_{i=1}^n (T_i)}</math>, onde n é a quantidade de medidas realizadas. | ||
| + | |||
| + | Para as incertezas das medidas, usa-se a expressão do [[:pt:desvio padrão|desvio padrão]]: | ||
| + | <math>\sigma_m = \sqrt{\dfrac{1} {n-1} \sum_{i=1}^n (T_i - T_m)^2}</math> | ||
| + | |||
| + | e o desvio padrão da média é calculado com: <math>\sigma_{media} = {\sigma_m\over n}</math> | ||
| + | ==== Obtenção de g através do procedimento 3 ==== | ||
| + | Para a determinação de g através do procedimento 3, é preciso ter feito o gráfico proposto anteriormente, que no caso é uma reta. | ||
| + | |||
| + | Analisando a expressão <math>T^2 = \dfrac{4\pi^2} {g} L</math>, observa-se que T² possui uma relação linear com L, no qual <math>4\pi^2\over g</math> é o coeficiente da reta estudada. | ||
| + | Graficamente, o coeficiente angular é calculado por: | ||
| + | <math>a = {{T^2_f - T^2_i}\over {L_f - L_i}}</math> | ||
| + | |||
| + | Manipulando algebricamente, g é dado por: | ||
| + | <math>g = 4\pi^2 \dfrac {(L_f - L_i)} {(T^2_f - T^2_i)}</math> | ||
| + | |||
| + | ==== Obtenção de g através do procedimento 4 ==== | ||
| + | |||
| + | Para a determinação de g, basta trabalhar algebricamente a expressão do período, obtendo: | ||
| + | |||
| + | <math>g = 4\pi^2 \dfrac{L}T^2</math> | ||
| + | |||
| + | === Observações === | ||
| + | |||
| + | Com a construção dos três gráficos propostos percebe-se que para diversos ângulos de oscilações, os períodos obtidos são bem próximos, logo, a aproximação para ângulos pequenos é válida para valores até 30°. Variando a massa do corpo preso ao fio do pêndulo é possível perceber pela construção dos gráficos e tabelas que o período pouco varia, ilustrando a independência do período com relação à massa. Já utilizando diferentes comprimentos de fios, observa-se a variação que este possui com o período. | ||
| − | + | Este experimento é interessante, pois é possível calcular g no local do experimento utilizando uma aparelhagem simples e não envolve cálculos muito difíceis. | |
Edição atual tal como às 20h45min de 11 de setembro de 2009
Conteúdo[ocultar] |
[editar] Experimento utilizando pêndulo simples
Os participantes do grupo são Débora, Diogo, Marcelo e Rafael
[editar] Objetivos da Experiência
O roteiro abaixo consiste de uma simples experiência com pêndulo simples para que se possa identificar as variáveis que influenciam no período de oscilação. Com este aparato é possível também calcular a aceleração gravidade no local onde o experimento é realizado. Faz parte do experimento a compreensão física das expressões envolvidas assim como os cálculos das incertezas que ocorrem nas medições.
[editar] Introdução Teórica
Galileu Galilei desenvolveu os primeiros estudos sistemáticos do movimento uniformemente acelerado e do movimento do pêndulo.O pêndulo simples consiste num fio, considerado inextensível, tendo uma de suas extremidades fixada num certo ponto, e a outra com uma massa concentrada. Quando afastado de sua posição de equilíbrio e solto, o pêndulo realizará oscilações em torno do eixo de rotação sob ação da gravidade. Perceba que além da força peso há a tração aplicada da corda na massa em questão.
Seu movimento representa, portanto, um movimento oscilatório, de modo que haja uma periodicidade, que é o tempo para realizar uma oscilação. Para pequenos deslocamentos, ou seja, para valores pequenos do ângulo de abertura (ângulo entre a vertical e o fio inextensível), a força resultante é proporcional ao deslocamento, porém de sentido oposto. Tal característica representa o movimento harmônico simples, daí, portanto pode se deduzir a fórmula do período do movimento.
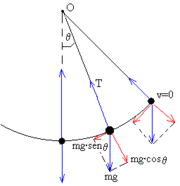
Para facilitar, escolhe-se um sistema de referência com um dos eixos tangencial à trajetória do pêndulo e o outro perpendicular, ou seja, está na direção radial.
Decompondo a força peso P, será obtido uma componente radial  e outra tangencial
e outra tangencial  .
A direção radial da força resultante é a força centrípeta necessária para manter a massa na ponta do fio na trajetória circular. Já na direção tangencial, a força é restauradora e faz com que a massa tende a retornar à posição de equilíbrio.
Esta força restauradora é dada por
.
A direção radial da força resultante é a força centrípeta necessária para manter a massa na ponta do fio na trajetória circular. Já na direção tangencial, a força é restauradora e faz com que a massa tende a retornar à posição de equilíbrio.
Esta força restauradora é dada por
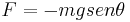
Para ângulos muito pequenos,  , para o ângulo medido em radianos.
, para o ângulo medido em radianos.
Assim 

Como 
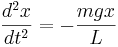
O termo  da expressão acima é constante e desempenha o mesmo papel da constante
da expressão acima é constante e desempenha o mesmo papel da constante  usada no cálculo da velocidade angular de um movimento harmônico.
Desta maneira:
usada no cálculo da velocidade angular de um movimento harmônico.
Desta maneira:

Sabemos que a velocidade angular pode ser expressa também por:
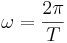
Igualando as duas expressões logo acima, obtém se o período de oscilação do pêndulo:

Sendo conhecido o período de oscilação e o comprimento do fio, basta isolar g para que possa calculá-lo:

[editar] Relação dos Materiais
- Bolinhas do pêndulo com as seguintes massas:
- 10g
- 33g
- 50g
- Fio inextensível
- Cronômetro
- Trena
[editar] Descrição Experimental
O experimento do pêndulo simples consistirá em quatro procedimentos para verificação dos parâmetros que influenciam o período de oscilação (T) e o cálculo da aceleração da gravidade.
No primeiro procedimento, será observado se o período de oscilação depende do ângulo inicial. Utilizando uma bolinha de qualquer uma das massas e um fio com 65,5 cm de comprimento, deve se adotar ângulos iniciais de 5°, 10°, 15°, 20° e 30°. Meça com um cronômetro o tempo gasto de dez oscilações, obtendo o período de uma única oscilação utilizando o cálculo de média simples. Com os dados obtidos construa uma tabela (1) e um gráfico (1) de Tx  onde
onde  é o ângulo de amplitude inicial. A partir dos dados, é possível calcular a incerteza (
é o ângulo de amplitude inicial. A partir dos dados, é possível calcular a incerteza ( ) de cada medida obtida, o valor médio (
) de cada medida obtida, o valor médio ( ) de oscilação e sua respectiva incerteza (
) de oscilação e sua respectiva incerteza ( ).
).
No segundo procedimento, será verificado se o período de oscilação do pêndulo depende da massa do corpo, no caso a bolinha. Adotando um ângulo inicial de amplitude de 10° e um fio com 65,5 cm de comprimento, utiliza-se no experimento bolinhas com 10 g, 33 g e 50 g. Realizando o mesmo método anterior para obter o período médio de oscilação de cada situação, obtém-se novamente o período de uma oscilação (com a ajuda de um cronômetro). Construa uma tabela (2) com os dados e um gráfico (2) de TxM, onde M é a massa de cada bolinha. Com os dados obtidos, calcula-se a incerteza de cada medida de período ( ), o tempo médio de uma oscilação (
), o tempo médio de uma oscilação ( ) e sua respectiva incerteza (
) e sua respectiva incerteza ( ).
).
No terceiro procedimento, será analisada a dependência do período de oscilação com o comprimento do fio. Utilizando uma das bolinhas e adotando um ângulo inicial de amplitude de 10°, muda-se o comprimento do fio em 30cm, 60cm e 90cm e execute o mesmo processo anterior para encontrar o período médio para cada uma das situações. Com os valores, monta-se outra tabela (3) e um respectivo gráfico, mas desta vez o gráfico não é de TxL e sim um de T²xL, pois assim, teoricamente, será encontrado uma reta, na qual o valor da aceleração da gravidade é extraído do coeficiente angular da mesma. Além disso, como das outras vezes, calcula-se as incertezas das medidas ( ), o valor do período médio (
), o valor do período médio ( ) de uma oscilação e sua incerteza (
) de uma oscilação e sua incerteza ( ).
).
O último procedimento é feito apenas para a determinação do valor da aceleração da gravidade através da expressão matemática apresentada anteriormente. Então usou-se novamente uma bolinha qualquer, um ângulo de amplitude de 10° e um fio com 50 cm de comprimento. Com a ajuda do cronômetro se faz a medida do período (a média calculada como nos outros procedimentos) e por fim o cálculo da aceleração da gravidade.
[editar] Cálculos envolvidos no experimento
Nos procedimentos 1,2 e 3, para o cálculo do período médio usa-se apenas uma média aritmética dos valores de períodos obtidos com a expressão:
 , onde n é a quantidade de medidas realizadas.
, onde n é a quantidade de medidas realizadas.
Para as incertezas das medidas, usa-se a expressão do desvio padrão:
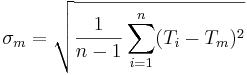
e o desvio padrão da média é calculado com: 
[editar] Obtenção de g através do procedimento 3
Para a determinação de g através do procedimento 3, é preciso ter feito o gráfico proposto anteriormente, que no caso é uma reta.
Analisando a expressão  , observa-se que T² possui uma relação linear com L, no qual
, observa-se que T² possui uma relação linear com L, no qual  é o coeficiente da reta estudada.
Graficamente, o coeficiente angular é calculado por:
é o coeficiente da reta estudada.
Graficamente, o coeficiente angular é calculado por:

Manipulando algebricamente, g é dado por:

[editar] Obtenção de g através do procedimento 4
Para a determinação de g, basta trabalhar algebricamente a expressão do período, obtendo:

[editar] Observações
Com a construção dos três gráficos propostos percebe-se que para diversos ângulos de oscilações, os períodos obtidos são bem próximos, logo, a aproximação para ângulos pequenos é válida para valores até 30°. Variando a massa do corpo preso ao fio do pêndulo é possível perceber pela construção dos gráficos e tabelas que o período pouco varia, ilustrando a independência do período com relação à massa. Já utilizando diferentes comprimentos de fios, observa-se a variação que este possui com o período.
Este experimento é interessante, pois é possível calcular g no local do experimento utilizando uma aparelhagem simples e não envolve cálculos muito difíceis.